06年度トライアル問題 問題9
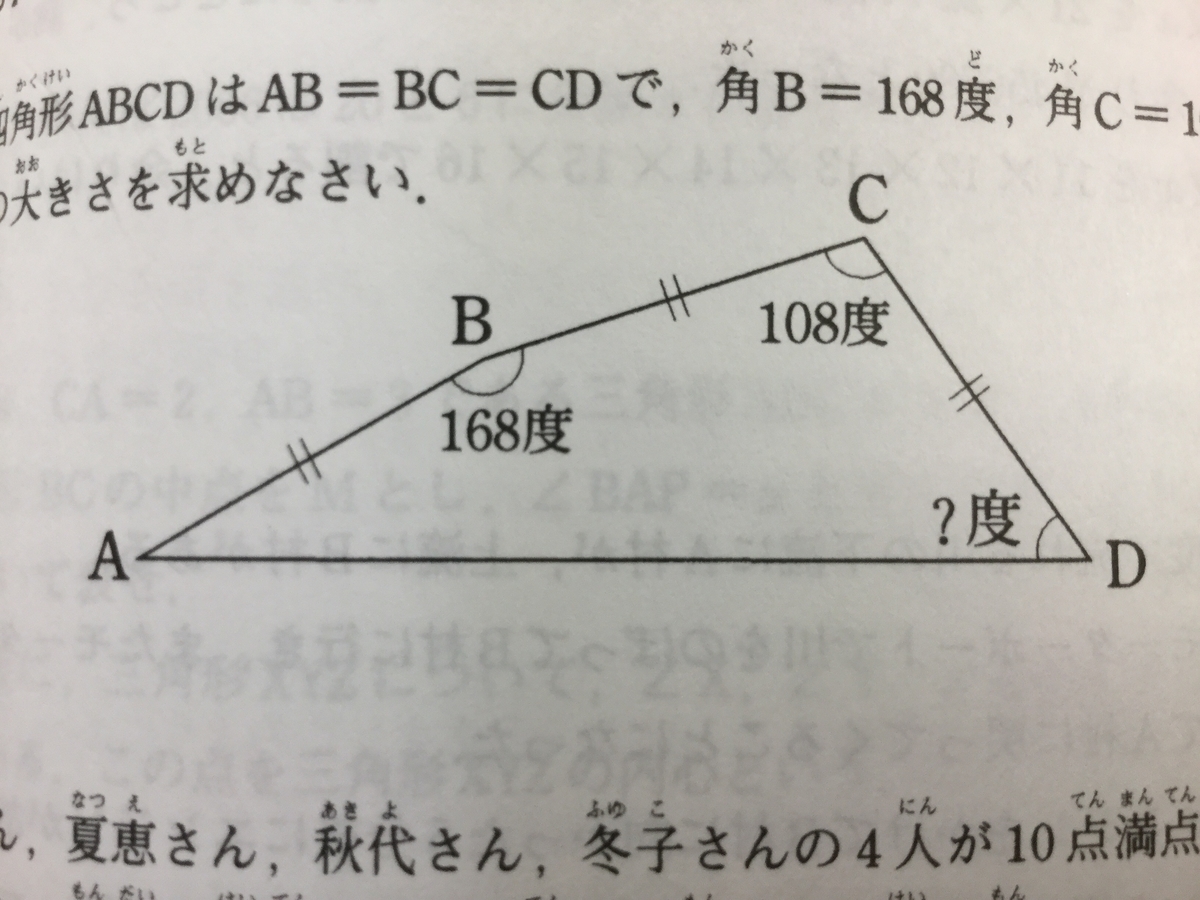
『図の四角形ABCDはAB=BC=CDで、角B=168度、角C=108度です。角Dの大きさを求めなさい。
 』
』
セットアップ
三角形、同じ大きさの角、同じ大きさの辺のディクショナリ(辞書)と、角の和、辺の和のリストをそれぞれ作成する。
まず三角形を探す。点に着目して、繋がっている点が他の繋がっている点と繋がっていたら、それは三角形。
着目した点。繋がっている点。 三角形。
A。B、D。
B。C。
triangle_lst = {} #今見ると辞書なのに名前にリストがあるのはマズいな
次に同じ大きさの角の辞書を作成する。
問題文の条件を見る。今回は迷ったが、試しに角ABCが168°とイコールと考えてみることにする。
対頂角や平行線の同位角や錯角は今のところ無し。
同じ大きさの角。
ABC、168。
BCD、108。
angle_equ = {
168 : 0,
"ABC" : 0,
108 : 1,
"BCD" : 1
}
次に同じ大きさの辺の辞書を作成する。
問題文の条件を見る。
同じ大きさの辺。
AB、BC、CD。
side_equ = {
"AB" : 0,
"BC" : 0,
"CD" : 0
}
角の和のリストを作る。
まず普通に点に着目する。しかし、2つ以上の角を持つような点は無し(厳密には360 - 角、みたいな感じであるが。しかしそれを記述しだすとアルファベット順という角への命名のルールが崩れる。必要になるまでは記述しない)。
次に三角形に着目して、外角を調べる。しかし三角形は無し。
sum_angle_lst = [ ]
辺の和のリストを作る。しかし辺が合わさったような辺は無し。
sum_side_lst = [ ]
この条件で三角形定理ループプログラムを回してみる。
角
0 : [168, 'ABC']
1 : [108, 'BCD']
角の和
辺
0 : ['AB', 'BC', 'CD']
辺の和
三角形そりゃそうだ。しかしエラーが発生しなくて良かった。
作図
以下4種類の作図をしていく。直接作図したもの以外に三角形や、あるいは正四角形や正五角形ができていたら、次の定理ループで角度が明らかになる可能性がある。
- 点と点を結んで線にする
- 点と点の距離の分だけ線を延長
- 2点と、その間の垂直線とどこか1辺の交点による、二等辺三角形の作図
- 同じ三角形を(同じ長さの辺の所に)作図
- 正四角形
- 正五角形
点と点を結んで線を作図する。
点に着目して、繋がっていない点を探す。点AとC、点BとD。
点AとCを結ぶ。
三角形を探す。辺ACに着目する。具体的には点AやCや辺ACによって発生した交点全てに着目する。
着目した点。繋がっている点。 結果。
A。B、C、D。 ABC、ACD。
C。B、D。
triangle_lst = {
"ABC" : ["BAC", "AB", "ABC", "BC", "ACB", "AC"],
"ACD" : ["CAD", "AC", "ACD", "CD", "ADC", "AD"]
}
新しく生まれた定義や対頂角や平行線の同位角や錯角を登録する。無し。
角の和を探す。点に着目する。
角の和。
BAC + CAD = BAD。
ACB + ACD = BCD。
sum_angle_lst = [
["BAC", "CAD", "BAD"],
["ACB", "ACD", "BCD"]
]
辺の和を探す。無し。
三角形定理ループプログラムを回してみる。
BAC == ACB
角
0 : [168, 'ABC']
1 : [108, 'BCD']
2 : ['BAC', 'ACB']
角の和
[2] + CAD == BAD
[2] + ACD == [1]
辺
0 : ['AB', 'BC', 'CD']
辺の和
三角形
ABC : [BAC[2], AB[0], ABC[0], BC[0], ACB[2], AC]
ACD : [CAD, AC, ACD, CD[0], ADC, AD]何が新しく分かったかというと、角の[2]と、角の和の2つ。しかしこれらには全て辺ACの絶対値?というか辺AC自体が入っており、元々の何かを明らかにした作図とは言えない。よって、この1ステップではこの作図には意味が無かったと言える。
点BとDを結ぶ。
三角形を探す。辺BD上の点に着目する。
着目した点。繋がっている点。 結果。
B。A、C、D。 ABD、BCD。
D。A、C。
triangle_lst = {
"ABD" : ["BAD", "AB", "ABD", "BD", "ADB", "AD"],
"BCD" : ["CBD", "BC", "BCD", "CD", "BDC", "BD"]
}
新しく生まれた定義や、対頂角や平行線の同位角や錯角を登録する。無い。
角の和を探す。辺BDによって生まれた角に関する所だけ追加すれば良い。辺BD上の点に着目すれば良いのではないか。
着目した点。 結果。
B。 ABD + CBD = 168。
D。 ADB + BDC = ADC。
sum_angle_lst = [
["ABD", "CBD", 168],
["ADB", "BDC", "ADC"]
]
辺の和を探す。無し。
三角形定理ループプログラムを回してみる。
CBD == BDC
角
0 : [168, 'ABC']
1 : [108, 'BCD']
2 : ['CBD', 'BDC']
角の和
[2] + ADB == ADC
[2] + ABD == [0]
辺
0 : ['AB', 'BC', 'CD']
辺の和
三角形
ABD : [BAD, AB[0], ABD, BD, ADB, AD]
BCD : [CBD[2], BC[0], BCD[1], CD[0], BDC[2], BD]よく見たら、一番上の結果だけ見れば良いのか。新しく作図したBD自体についてしか明らかになっていないので、この作図は少なくともこのステップでは意味が無かった。
で、点と点の分だけ辺を延長だけど、それをすることで新しく三角形が発生するということが無いので、スルーする。機械的に三角形が発生しているか調べる時は、その作図をすることで新しく生まれる点に着目して三角形を探せば良いと思う。
で、次に二等辺三角形の作図だけど、二等分線以外のパターンも考えられるな。ABと同じ長さの辺を点BからADの上に作図する、というのもあっても良いのではないか。
というか、例えば二等分線がどこと交わるか、分からないんだよな。でも、今の所は、作図はあくまでアナログというか、人間がやるような論理的ではない別工程なのだし、長くなるけどやってみるか。
まず辺ABに着目する。
辺ABの二等分線と辺ADの交点で、二等辺三角形を作図する場合を考えてみる。
交点をEとする。
triangle_lst = {
"ABE" : ["BAE", "AB", "ABE", "BE", "AEB", "AE"]
}
angle_equ = {
168 : 0,
"ABC" : 0,
108 : 1,
"BCD" : 1,
"BAE" : 2,
"ABE" : 2
}
side_equ = {
"AB" : 0,
"BC" : 0,
"CD" : 0,
"AE" : 1,
"BE" : 1
}
sum_angle_lst = [
["AEB", "BED", 180],
["ABE", "CBE", 168]
]
sum_side_lst = [
["AE", "DE", "AD"]
]
角
0 : [168, 'ABC']
1 : [108, 'BCD']
2 : ['BAE', 'ABE']
角の和
AEB + BED == 180
[2] + CBE == [0]
辺
0 : ['AB', 'BC', 'CD']
1 : ['AE', 'BE']
辺の和
[1] + DE == AD
三角形
ABE : [BAE[2], AB[0], ABE[2], BE[1], AEB, AE[1]]ってそうか、三角形が2つは無いと駄目なのか。
じゃあ、次はBCの上に二等辺三角形でも作ってみるか。
triangle_lst = {
"ABE" : ["BAE", "AB", "ABE", "BE", "AEB", "AE"],
"BCE" : ["CBE", "BC", "BCE", "CE", "BEC", "BE"],
"CDE" : ["DCE", "CD", "CDE", "DE", "CED", "CE"]
}
angle_equ = {
168 : 0,
"ABC" : 0,
108 : 1,
"BCD" : 1,
"CBE" : 2,
"BCE" : 2
}
side_equ = {
"AB" : 0,
"BC" : 0,
"CD" : 0,
"BE" : 1,
"CE" : 1
}
sum_angle_lst = [
["ABE", "CBE", "ABC"],
["BCE", "DCE", "BCD"],
["AEB", "BEC", "AEC"],
["BEC", "CED", "BED"],
["AEC", "CED", 180],
["BED", "AEB", 180]
]
sum_side_lst = [
["AE", "DE", "AD"]
]
角
0 : [168, 'ABC']
1 : [108, 'BCD']
2 : ['CBE', 'BCE']
角の和
AEC + CED == 180
BED + AEB == 180
AEB + BEC == AEC
BEC + CED == BED
[2] + ABE == [0]
[2] + DCE == [1]
辺
0 : ['AB', 'BC', 'CD']
1 : ['BE', 'CE']
辺の和
AE + DE == AD
三角形
ABE : [BAE, AB[0], ABE, BE[1], AEB, AE]
BCE : [CBE[2], BC[0], BCE[2], CE[1], BEC, BE[1]]
CDE : [DCE, CD[0], CDE, DE, CED, CE[1]]何にも無いな。本当にこれで良いのかね。
同じ三角形の作図。と書いたけど、同じ図形の作図だな。同じ長さの辺の上に作図する。
まずBCを底辺として、そのまま左右に反転させた図形。新しい点Dだった点をE、点Aだった点をF。更に辺CDだった辺とADの交点をG、辺ADだった辺と辺ADをH、辺ADだった辺と辺CDの交点をIとする。(手元に書いた)
triangle_lst = {
"ABG" : ["BAG", "AB", "ABG", "BG", "AGB", "AG"],
"EGH" : ["GEH", "EG", "EGH", "GH", "EHG", "EH"],
"DHI" : ["HDI", "DH", "DHI", "HI", "DIH", "DI"],
"CFI" : ["FCI", "CF", "CFI", "FI", "CIF", "CI"]
}
定義と、あと対頂角も登録しないとな。並行もありそうだけど、角度から並行を見つける機能も必要かな?
angle_equ = {
168 : 0,
"ABC" : 0,
"BCF" : 0,
108 : 1,
"BCI" : 1,
"CBG" : 1,
"BAG" : 2,
"CFI" : 2,
"GEH" : 3,
"HDI" : 3,
"AGB" : 4,
"EGH" : 4,
"AGE" : 5,
"BGH" : 5,
"CIF" : 6,
"DIH" : 6,
"CIH" : 7,
"DIF" : 7,
"GHI" : 8,
"DHE" : 8,
"EHG" : 9,
"DHI" : 9
}
side_equ = {
"AB" : 0,
"BC" : 0,
"CD" : 0,
"CF" : 0,
"BE" : 0,
"AD" : 1,
"EF" : 1
}
じゃあ点に着目して、角の和を見つけていくかな。
sum_angle_lst = [
["ABG", "CBG", "ABC"],
["BCI", "FCI", "BCF"],
["AGB", "BGH", 180],
["GHI", "DHI", 180],
["CIH", "CIF", 180]
]
辺の和はどうやって見つけようかな。やっぱり点に着目していくかな。
sum_side_lst = [
["BG", "EG", "BE"],
["AG", "GH", "AH"],
["AG", "DG", "AD"],
["GH", "DH", "DG"],
["AH", "DH", "AD"],
["EH", "HI", "EI"],
["EH", "FH", "EF"],
["CI", "DI", "CD"],
["HI", "FI", "FH"],
["FI", "EI", "EF"]
]
いやちょっと、なんだこれって感じだけど。三角形定理ループプログラムを回してみる。
angle_equ[4] == angle_equ[6]
FCI == ABG
BG == CI
AG == FI
angle_equ[5] == angle_equ[7]
EG == DI
DG == EI
GH == HI
EH == DH
AH == FH
角
0 : [168, 'ABC', 'BCF']
1 : [108, 'BCI', 'CBG']
2 : ['BAG', 'CFI']
3 : ['GEH', 'HDI']
4 : ['AGB', 'EGH', 'CIF', 'DIH']
5 : ['AGE', 'BGH', 'CIH', 'DIF']
8 : ['GHI', 'DHE']
9 : ['EHG', 'DHI']
10 : ['FCI', 'ABG']
角の和
[4] + [5] == 180
[8] + [9] == 180
[1] + [10] == [0]
辺
0 : ['AB', 'BC', 'CD', 'CF', 'BE']
1 : ['AD', 'EF']
2 : ['BG', 'CI']
3 : ['AG', 'FI']
4 : ['EG', 'DI']
5 : ['DG', 'EI']
6 : ['GH', 'HI']
7 : ['EH', 'DH']
8 : ['AH', 'FH']
辺の和
[2] + [4] == [0]
[7] + [8] == [1]
[3] + [5] == [1]
[6] + [7] == [5]
[3] + [6] == [8]
三角形
ABG : [BAG[2], AB[0], ABG[10], BG[2], AGB[4], AG[3]]
EGH : [GEH[3], EG[4], EGH[4], GH[6], EHG[9], EH[7]]
DHI : [HDI[3], DH[7], DHI[9], HI[6], DIH[4], DI[4]]
CFI : [FCI[10], CF[0], CFI[2], FI[3], CIF[4], CI[2]]結局、分かりにくいけど、角AがBAGで[2]、角DがHDIで[3]、角Bが168の[0]で、角Cが108の[1]なんで、何も分かってないと言える。
これちょっとどうしようかな。まあ、1ステップだけ全部やるか。作図がどんな感じか分からないと、自動化することもできない。
順番がゴチャゴチャな気もするけど、次はABとBCを入れ替えるような作図をやってみようか。
手元で描いてみた。どの辺とどの辺で交点ができるか分からないっていうのが、プログラムを作る上での壁なんだよな。なぜ、ADだった辺とADはクロスするのだろう。ABCDというクラスタがあって、その外側からアクセスしているから?、いや違うな。ABやBCではあり得ず、また点Cを端にしているという点でCDでもあり得ないから?、いや包み込むような場合があり得るな。点Cに対しては角度が浅く、点Aに対しては角度が大きいから?、あり得るような気もする。図形と図形なら、そういう考え方ができる場合もあるか?、でも共有していない場合も交点が発生する場合はあり得る。
これは小学生が現に解いている問題なわけで、必ず論理的な答えはあるはず。そうでなければ部分的には出題者のミスとして言い切れるはず。そのどちらかは分かるはずだと思っているが。
この作図に限っては、2つの辺のどちらで交点が発生するかは言い切れる。そういう交点の判断例を集めることが重要かと思う。
では、新しく追加した点Dだった点をE、新しい交点をFと名付ける。
AE上の点と、CE上の点に着目して三角形を探す。
triangle_lst = {
"AEF" : ["EAF", "AE", "AEF", "EF", "AFE", "AF"],
"CDF" : ["DCF", "CD", "CDF", "DF", "CFD", "CF"]
}
コピー元の定義と(忘れていたけどコピー元との対応と)、対頂角と平行線の同位角と錯角を記載する。あと、角の名前を修正する。
angle_equ = {
168 : 0,
"ABC" : 0,
108 : 1,
"BCD" : 1,
"BAE" : 1,
"AFE" : 2,
"CFD" : 2,
"AFC" : 3,
"DFE" : 3,
"AEF" : 4,
"CDF" : 4,
"BAF" : 5,
"BCF" : 5
}
side_equ = {
"AB" : 0,
"BC" : 0,
"CD" : 0,
"AE" : 0,
"AD" : 1,
"CE" : 1
}
点に着目して単純な角の和と、三角形に着目して外角の性質による角の和を記載する。
sum_angle_lst = [
["BAF", "EAF", "BAE"],
["BCF", "DCF", "BCD"],
["AFE", "AFC", 180],
["EAF", "AEF", "AFC"],
["DCF", "CDF", "AFC"]
]
点あるいは点から伸びている辺に着目して、辺の和を記載する。
sum_side_lst = [
["CF", "EF", "CE"],
["AF", "DF", "AD"]
]
三角形定理ループプログラムを回す。
EAF == DCF
EF == DF
AF == CF
角
0 : [168, 'ABC']
1 : [108, 'BCD', 'BAE']
2 : ['AFE', 'CFD']
3 : ['AFC', 'DFE']
4 : ['AEF', 'CDF']
5 : ['BAF', 'BCF']
6 : ['EAF', 'DCF']
角の和
[2] + [3] == 180
[5] + [6] == [1]
[4] + [6] == [3]
辺
0 : ['AB', 'BC', 'CD', 'AE']
1 : ['AD', 'CE']
2 : ['EF', 'DF']
3 : ['AF', 'CF']
辺の和
[2] + [3] == [1]
三角形
AEF : [EAF[6], AE[0], AEF[4], EF[2], AFE[2], AF[3]]
CDF : [DCF[6], CD[0], CDF[4], DF[2], CFD[2], CF[3]]新しく明らかになったものが無かったので、意味無し。でも、やっぱり論点はどの辺とどの辺で交点ができるかの判定だと思う。
似たようなパターンで、BCとCDで入れ替えてみる。気付いたけど、同じ長さの辺と辺の関係を考えれば、つまり例えばBCを全部考えたら、残りの辺ではBCについて考える必要は無さそうだ。
交点の判定も似たようなパターンで、共有した2点の角度が互い違いで交点が発生することは確定し、しかも2辺なのでどちらの辺で発生するのかも確定する。
新しい元AをE、元ADとADで発生する交点をFとする。
新しく追加した辺BE・辺DE上の点に着目して三角形を探していく。
triangle_lst = {
"ABF" : ["BAF", "AB", "ABF", "BF", "AFB", "AF"],
"DEF" : ["EDF", "DE", "DEF", "EF", "DFE", "DF"]
}
対応する角や辺と、対頂角と、平行線の同位角と錯角を登録していく。角の名前も修正する。
angle_equ = {
168 : 0,
"ABC" : 0,
"CDE" : 0,
108 : 1,
"BCD" : 1,
"BAF" : 2,
"DEF" : 2,
"CDF" : 3,
"CBF" : 3,
"AFB" : 4,
"DFE" : 4,
"BFD" : 5,
"AFE" : 5
}
side_equ = {
"AB" : 0,
"BC" : 0,
"CD" : 0,
"DE" : 0,
"AD" : 1,
"BE" : 1
}
新しく追加した辺BE・辺DE上の点に着目して、新しい角の和を探していく。また三角形に着目して外角の法則による角の和を探していく。
sum_angle_lst = [
["ABF", "CBF", "ABC"],
["CDF", "EDF", "CDE"],
["AFB", "BFD", 180],
["BAF", "ABF", "BFD"],
["EDF", "DEF", "BFD"]
]
で辺の和だけど、角の和で180°が見つかった、"AFB"と"BFD"の要であるFについてだけ探せば良いのではないか。まあどうでも良い話ではあるけども。
sum_side_lst = [
["AF", "DF", "AD"],
["BF", "EF", "BE"]
]
三角形定理ループプログラムを回してみる。
ABF == EDF
BF == DF
AF == EF
角
0 : [168, 'ABC', 'CDE']
1 : [108, 'BCD']
2 : ['BAF', 'DEF']
3 : ['CDF', 'CBF']
4 : ['AFB', 'DFE']
5 : ['BFD', 'AFE']
6 : ['ABF', 'EDF']
角の和
[4] + [5] == 180
[3] + [6] == [0]
[2] + [6] == [5]
辺
0 : ['AB', 'BC', 'CD', 'DE']
1 : ['AD', 'BE']
2 : ['BF', 'DF']
3 : ['AF', 'EF']
辺の和
[2] + [3] == [1]
三角形
ABF : [BAF[2], AB[0], ABF[6], BF[2], AFB[4], AF[3]]
DEF : [EDF[6], DE[0], DEF[2], EF[3], DFE[4], DF[2]]実は一回ミスをして妙な結果になったんだが、まあ修正した。何も無し。
次はBCをCDに反転させずに重ねるような作図を考えてみる。
角Bと角Cだと角Bの方が大きく、また角Cと角Dでも角Cの方が大きい(なぜなら四角形は内角が360°で残りは84°しか無いから)。
この場合は、交点は2つか0かのどちらかだろう。直感的には、元ADがABとBCのどちらに交わるかが特に分からない。
困ったなあ。というかこれ、五角形とか六角形とかだったらどうするんだろう。
一つの方法としては、交点がどこで発生するか分からない場合は、そもそも交点を考えないというのがある。その場合、その交点による三角形や、角の和や辺の和などは作られない。おそらくだが、その場合でも問題無く三角形定理ループは回せる。しかし、その方法を取るならば、だからこそどの場合にどの辺と辺で交点が発生するのかを明らかにしなければならない。
暫定的に、分からない、としてみようか。それで問題が出るまで待つことにしよう。おそらく、三角関数(直角の場合しか憶えてないが、多分そういうものがある)のようなものが必要になるのではないかと思うが。その場合は、その関数がどういう風に導かれるかが問題になる。
分からないものは交点を考えないとして、少なくとも2つ以上三角形は生まれないので、この場合は考えない。
よく考えたら、交点の検討こそがメインであって、その後の対応する角や辺の登録だとか、三角形を探したりするのだとかは、もはやオマケでしかないのではないか。
順番が滅茶苦茶だけど、次はBCをABにそのままズラしたような作図を検討する。
角Bの方が角Aより大きく、逆に角Cは角Bより小さいので、おそらく交わる回数は1回か3回だろう。手元で描いてみたら、3回交わったら、三角形が4つできることもありそうだが。
元のADに交わるとは限らない、例えばBCとADを縮めれば、元CDと新しいCDで交わることもあり得るし、元ADと新しいCDもあり得る。元CDと新しいADだけというのは無理だろうが。
元AD 新しいAD ○
元AD 新しいCD ○
元CD 新しいAD ×
元CD 新しいCD ○
元AD 新しいADとCD ×
元CD 新しいADとCD 更にその場合は元ADと新しいAD ○
いやだからどうしたという話で、ちょっと迷走しているな。
とにかく、絶対にどこかの辺に交点ができるということは無いということじゃないか。
まあ別に、交点が分からないから交点を加えないとして、今のところは解答のプロセスには影響は無い。
3辺以上になると、角度が完全に内側にあっても外側にあっても、互い違いになっていても、分からないということが分かったんじゃないか。
補助線を引いて三角形にしたりして考えてみても、どうも何かの条件で、どの辺とどの辺で交点が発生するかを特定するのは難しいのではないか。いや分からないが。
2辺以内という条件で、支障が出るのを待つか。
うーん、3つの辺なら、一方の対角線と、もう一方の逆側の普通の線で、交わったら、とかそういう条件はどうだろう。対角線と交わった場合、対角線側を形作るどちらか1辺と交わっている、とか。
更にその対角線側のどちらの辺と交わっているかも、反対の対角線と、その普通の線で角度を比べて、浅いか深いかみたいな。
いや、交わらない場合が判定できないのではないか。いや、しかしそれも、もう一方でも調べて照らし合わせれば良いか?
いやいやいや、そもそも交わるかが分からないからな。
いや考えてみても、やっぱりちょっと無理だな。
やっぱりとりあえず2辺以内だったら、互い違いかを見ることで、辺が交わるか、そしてどちらの辺と辺が交わるかが分かる、という所に留めておくべきではないか。支障が出た時に、その問題ではどう考えているかを見れば良い。
ということは、ABとCDを合わせるのは、お互いに3辺同士だから、どの辺に交点ができるかは分からないということになるのか?
ADを左右に反転させるのも、3辺同士だから、どの辺に交点ができるかは分からない?
まあ確かにこの問題では支障は無いが。しかしどこかで支障が出そうな気はするな。いやその時は答えを見て、その論理をそのままパクれば良いのか。でも多分、三角形の形が確定した後に、あの表みたいなのを見るのが正解なんだと思うなあ。
一番の問題である、作図した時に辺と辺の交点がどこにできるか問題は、とりあえず「3辺以上だったら交点は考えない」で良いか。
まあでも作業の流れをハッキリさせる必要があるんで、このまま2ステップ目に進むか。