06年度トライアル問題 問題9
『図の四角形ABCDはAB=BC=CDで、角B=168度、角C=108度です。角Dの大きさを求めなさい。
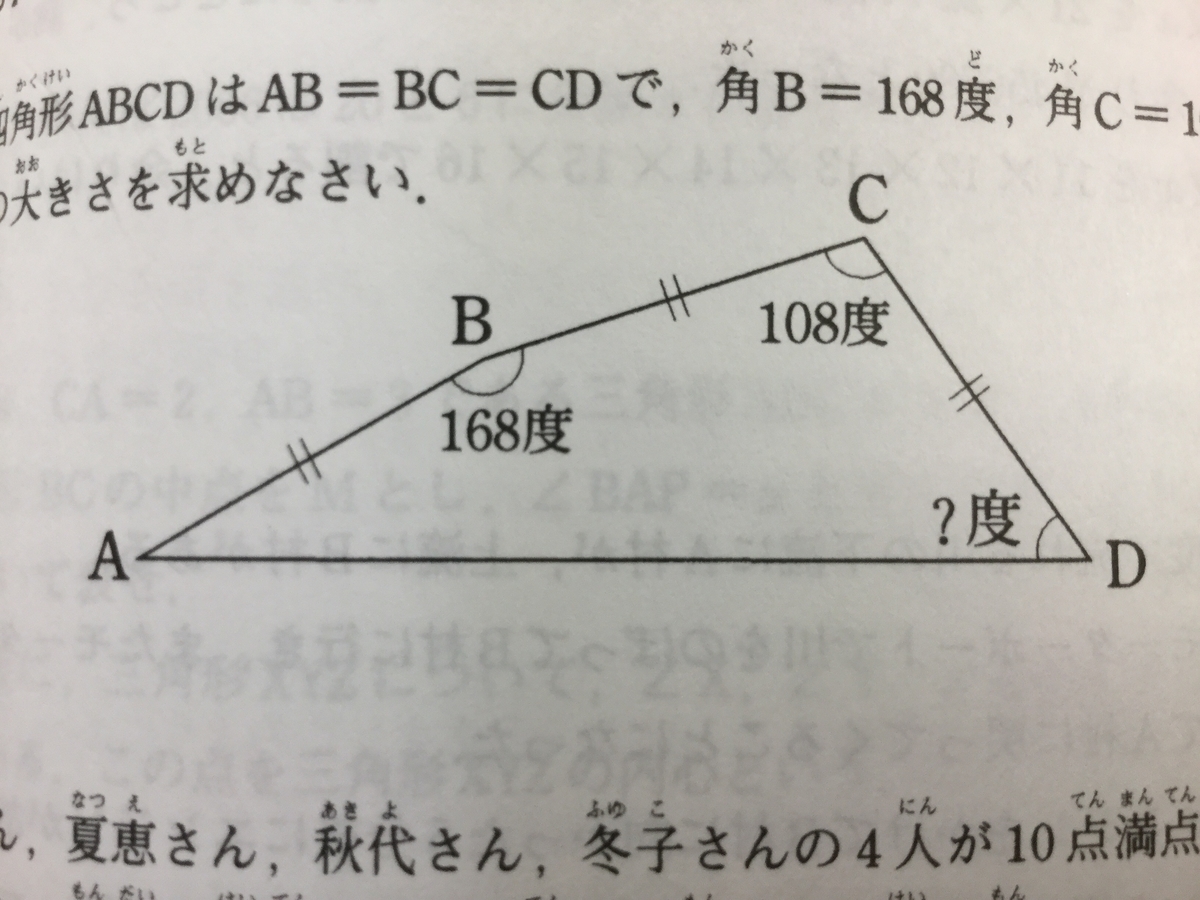 』
』
前回の続き。
作図
以下5種類の作図をしていく。直接作図したもの以外に三角形や、あるいは正四角形や正五角形ができていたら、次の定理ループで角度が明らかになる可能性がある。
- 点と点を結んで線にする
- 点と点の距離の分だけ線を延長
- 2点と、その間の垂直線とどこか1辺の交点による、二等辺三角形の作図
- ある1辺と同じ長さの辺を別の辺に落とすことによる二等辺三角形の作図
- 同じ図形の作図(同じ長さの辺の所に)
- 正四角形
- 正五角形
じゃあ、1ステップ目の同じ図形の作図から。
それぞれの辺ごとに、そのまま点の位置を逆転させるのと、辺を軸に返すのと、辺を軸に返した上で点の位置を逆転させるのとで、3種類ある。
いや、同じ長さの辺とかがあるから、その同じ長さの辺による組み合わせもあるのか。
複製して、辺ABの位置をどこかに移す場合から考える。
まず対象はAB、BC、CDだが、外側に作っても新しく三角形が作られないので、本当は外側への2種類の作図は考えても意味は無い。
ABを軸にそのまま返したような作図の場合で考えると、点CとDに対応して、点EとFを追加する。そして辺をgraphに登録し、対応するangle_equとside_equを登録する。
辺BEは、角ABCのネガティブ側、角ABC_nを割っている。角ABEも168°で、角CBEも360°以下なので、ABE + CBE = ABC_nと登録できる。
辺AFは、角BADのネガティブ側、角BAD_nを割っている。角BAFはポジティブ(つまり180°以下)なわけだが、もう一つの角は、いや、その2つの角がそれぞれ84°以下なので、ネガティブだと断定できるわけか。BAF + DAF_n = BAD_n。
しかし、また比較が出てきた。どうも作図において、比較を登録しておく機能は必要みたいだ。
また、今回は判明したが、判明しない場合もあり得る。そうすると、例えば角ABCと角ABC_nという表記では無く、発見された順にABC_1とABC_2と表記するべきなのかもしれない。ABC_1 + ABC_2 = 360で、ポジティブだと分かったら例えばABC_2 < 180。まあ試してみるか。
今回は始まったばかりなんで、次の作図から試してみることにしよう。
でとにかく、複製してABの辺を移すのの対象は、ABとBCとCDの内側ということになる。
ABのAとBを反転させて移す場合、同じようにCとDだったのをEとFと名付けるとして、さっき言ったように複製することになる。角A < 角Bなので、元々の角ABCは割られることになり、ABF_1 + CBF_1 = ABC_1、割られる角がABC_1 < 180なので、ABF_1 < 180、CBF_1 < 180だ。
また元々の角BADはむしろ割る側になる。BAD_1 + DAE_1 = BAE_1、これも同じく割られる角がBAE_1 < 180なので、BAD_1 < 180、BAE_1 < 180。
うーん、ちょっと分かりにくい気もするな。でも当初はBAD_1やBAD_2とかいう風に名付けて、分かり次第BAD_pやBAD_nと名付けるか?どうしようかな。
交点が分からない状態は、3D空間での作図を想像して貰えれば概念的には近いと思う。必ず交点を見つける必要があるというわけでは無い。
で、この時に、新しく複製した元ADと元CDで、どちらに交点が発生するかは、俺の記憶が正しければ分からないという結論だったような。実際にはADと元ADが交わってそれで終わりなんだろうが。
ADと元ADは、辺と辺が交わるかという問題なんだろうな。CDと元ADも、BCを介して同じ問いに持ち込むことができるか。ADと元CDも、だとしたらきっと似たような感じ。CDと元CDはどうなんだろうな。ABCを固めてACが明らかになればって感じなのか?
しかし、その辺と辺が交わるか、っていうのが分からないのだよな。休憩(別に何度でも休憩はしているわけだが)。
今までの作図の道具まとめ
ちょっといきなり脱線するようだけど、今までの作図における道具をまとめてみた。そういうことをしないと考えがまとまらない。
5種類ある作図のうち、点と点を結んで線にするのと、点と点の距離の分だけ線を延長は、特に無し。特に後者はまだ出てきてないだけかもしれない。
辺の垂直二等分線による二等辺三角形の作図
- 垂直二等分線は、角度の小さい方と交わる
- 垂直二等分線は、辺が長い方と交わる
- 垂直二等分線で、クラスタのどこにも交わらないなら、残りに交わる
同じ長さの辺を繋がっている辺に落とすことによる二等辺三角形の作図
条件は2つある
1・繋がっている辺との角が90°以下
説明1:それ以上だと垂線より長くなって届かない
説明2:同じ長さの辺を落とす時に、元々の境目が90°以上で、二等辺三角形で180°以上になるので無理
説明3:同じ長さの辺を落とす時に、一番端が短いものは、どんどん元の辺によっていって、元の辺の位置で一致するので無理
2・底辺の中心と頂点の位置関係
- 底辺の中心と頂点を結んだ時の頂点角の角度と、頂点から垂線を垂らした時の頂点角の角度(180 - 90 - 元の2辺の角度) 後者が大きければ無理
- あるいは、底辺の半分と、垂線を垂らした時の辺の長さ 後者が大きければ無理
※ちなみに他にも「底辺の半分と頂点を結んだ長さと、垂線の長さを比較する」という間違った説明があった
同じ図形の同じ長さの辺への作図
- クラスタの底辺を重ね合わせた時に、底辺の角度が互い違いになっているなら、どこかで交点が発生する。2辺ならどちらの辺が交わるかも明らかになる(なぜなら二等辺三角形だと角度が半々になって、そこからは辺が長い方が角度は浅くなるから)(3辺以上になると、分からないのではないか)
- 図形を重ね合わせた時に、一つ一つの辺の関係を問うていく。1つの辺を挟んで存在する2つの辺と辺は交わるか。
実装課題
- クラスタの登録
クラスタを対角線で突っ切っている場合、真ん中に交点ができる
- 角の具体的な足し算引き算も実装しなければならないのではないか、内角など
角1 + 角2 + 角3 = 180。
x + 2*x + 2*x = 180。
A + B = 72.5、B + C = 78、A + B + C = 121。B = 29.5。
- 比較も実装したい。具体的な数値が分からない状態での上下の判断に特に注目
内角から判断して、何度以下かは分かったりする
どちらが長いかの判断で、元々2つの辺が等しく、その間の角が60°以上の場合、下の辺はそれらより長い、60°以下の場合、下の辺はそれらより短い
- 角の名前の変更 ABC_1・ABC_2から、どちらかが180°以下と判明し次第、ABC_p・ABC_n。
- 面積比と底辺比 でもこれはどうなんだろう。
作図の問題に戻る
で、その1辺を挟んだ2辺が交わるかだけど、これは三角関数?が無いと分からないんじゃないかなあ、多分。
まあだからつまり、元ABを、BCやCDに、そのままと反転と2通りずつ作図していくのも、これは分からないという結論になる。つまり作図はしない。
いや、後から振り返ると間違いで、角Bを軸にABとBCを入れ替えるような作図は、2辺なのでどちらに交わるか分かる。
そのようにABとBCを入れ替える場合、BCとCDを入れ替える場合の2種類を、実際に試してみる。
まずABとBCを入れ替えるような作図。
まず一番最初のスタート地点を用意する。
graph = {
"A" : [
[["B"], []],
[["D"], []]
]
,
"B" : [
[["A"], []],
[["C"], []]
]
,
"C" : [
[["B"], []],
[["D"], []]
]
,
"D" : [
[["A"], []],
[["C"], []]
]
}
triangle_lst = {
}
cluster_lst = [
["BAD_p", "ABC_p", "BCD_p", "ADC_p"] #こういうものは自動化したいが、これは自明では無く問題文の情報なので記述する
]
angle_equ = [
["ABC_p", 168], #しかしこのpというのはどうなんだろうな。普通の無しの方が分かりやすくないかな、試してはみるけど
["BCD_p", 108]
]
side_equ = [
["AB", "BC", "CD"]
]
angle_less_than = [
]
side_less_than = [
]
sum_angle_lst = [ #2つ以上の足し算も記述することにする。答えも2つ以上にするかは、迷うけど、そのつもりで行く
]
sum_side_lst = [
]
なんか随分、必要なリストが増えてしまった。今は試行錯誤の段階で、必要無くなったら減らすけど、おそらく必要ではないかと思う。
で、考えたけど、クラスタからsum_angle_lstを読み取る。あと、pがある分のnを登録する。
あと、angle_less_thanも更新できそうだ。これからは上から確認していくことにしよう。
sum_angle_lst = [ #左辺の総和 = 右辺の総和 [["BAD_p", "ABC_p", "BCD_p", "ADC_p"], [360]], [["BAD_p", "BAD_n"], [360]], [["ABC_p", "ABC_n"], [360]], [["BCD_p", "BCD_n"], [360]], [["ADC_p", "ADC_n"], [360]] ] angle_less_than = [ #左辺の総和 < 右辺の総和 [["BAD_p"], [84]], [["ADC_p"], [84]] ]
本当の流れはどうなるかは分からないけど、とりあえず上から確認していったし、三角形も無いので、次の作図に進むことにする。
ABとBCを入れ替えたような図を作図し、元DをEと名付ける。いや違うな、ABをCBと対応するように作図し、被ったものは消すか。ということは、元Cに対応するのがEで、元Dに対応するのがFか。
いや書いてみたけど、まだプログラムみたいに厳密に記述するのは早いな。流れすら確立して無いのだから。
まず元Aと元Dの辺、つまりCFが、点Cに属する角を、それぞれ割っているかを確認する必要がある。
角BCD_pと角BCF_pを比較して、BCD_pの方が大きいので、BCD_pを割ったと判断する。
…もう駄目だと思って昼寝していたけど、これって元の体系に合流できないかな。なんか逃げっぽいけど。いつか合流させたいと思っていたけど、今のタイミングで合流して良いんじゃないかな。
まあ明日一回だけ、それを試してみようかな。ABとBCを入れ替える場合を。いや、逃げかなこれは。