06年度トライアル問題 問題9
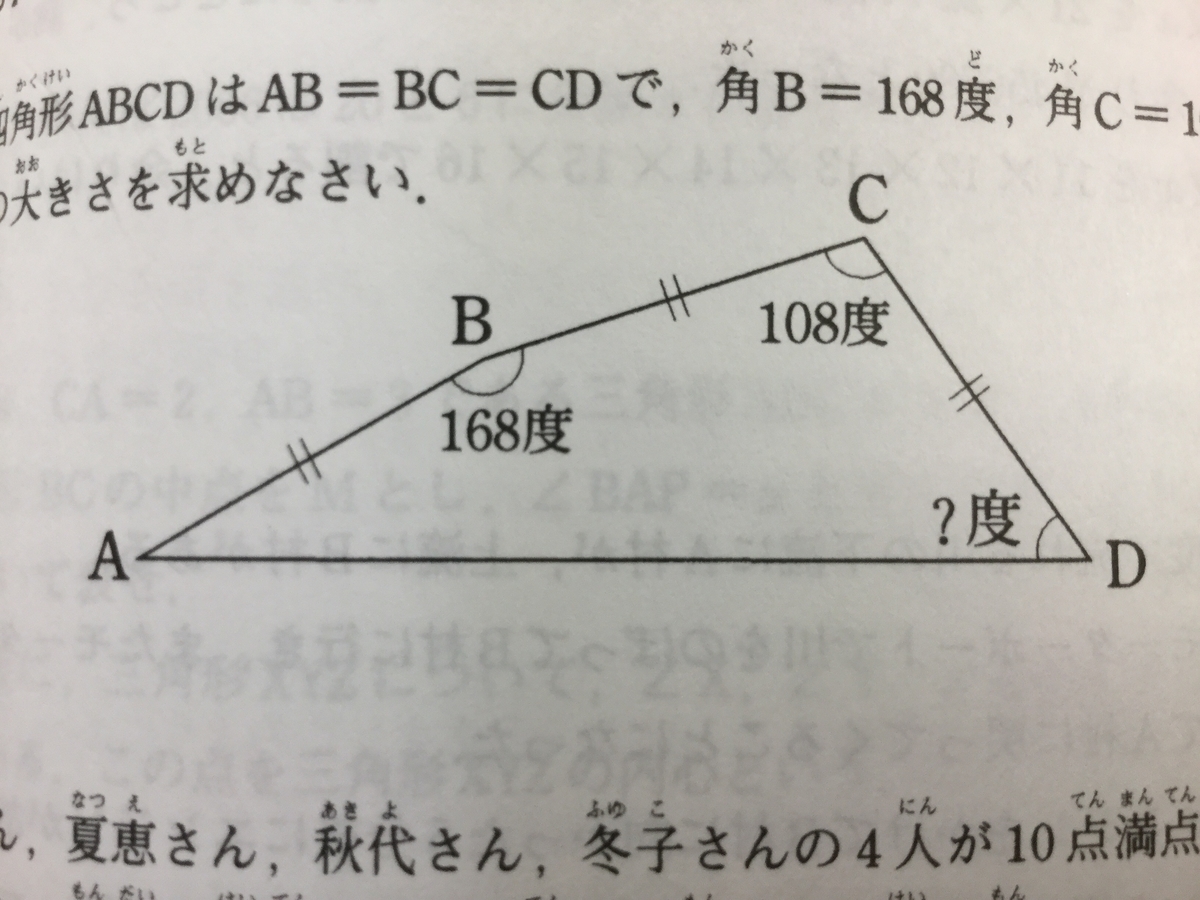
『図の四角形ABCDはAB=BC=CDで、角B=168度、角C=108度です。角Dの大きさを求めなさい。
 』
』
どうしよう。一旦最初からやろうかな?そっちの方が分かりやすい気がする。まだ自然言語中心で。
作図
以下5種類の作図をしていく。直接作図したもの以外に三角形や、あるいは正四角形や正五角形ができていたら、次の定理ループで角度が明らかになる可能性がある。
- 点と点を結んで線にする
- 点と点の距離の分だけ線を延長
- 2点と、その間の垂直線とどこか1辺の交点による、二等辺三角形の作図
- ある1辺と同じ長さの辺を別の辺に落とすことによる二等辺三角形の作図
- 同じ図形の作図(同じ長さの辺の所に)
- 正四角形
- 正五角形
じゃあ一番最初の状態を。
graph := [
"A" : [
[["B"], []],
[["D"], []]
]
,
"B" : [
[["A"], []],
[["C"], []]
]
,
"C" : [
[["B"], []],
[["D"], []]
]
,
"D" : [
[["A"], []],
[["C"], []]
]
];
"ABC_p" == 168;
"BCD_p" == 108;
"AB" == "BC" == "CD";
"ABC_p" + "ABC_n" == 360;
"BCD_p" + "BCD_n" == 360;
"BAD_p" + "BAD_n" == 360;
"ADC_p" + "ADC_n" == 360;
triangle_lst := [
];
cluster_lst := [
["BAD_p", "ABC_p", "BCD_p", "ADC_p"] #ネガティブ同士でもクラスターだと考えるか?いや無いな、辺を追加した時に意味不明になる。
];これは三角形定理ループを回しても、答えには行き着かないんだった。
じゃあまず、1ステップ目のAとCを繋ぐ作図をやってみる。
まずgraphでAとCを繋ぐ。更に2次元の問題なので、繋ぐだけで無く、既存の角を割る動作でもあるはずだ。
点Aだと、BADのポジティブかネガティブを割り、更に新しくBAC・DACのポジティブ・ネガティブが発生しなければいけない。
cluster_lstを見ると、点Aと点Cが登録してあるクラスタがあり(下を参照)、点AとCは結ばれておらず、しかもクラスタのどの角もポジティブなので、点AとCはクラスターの内部で結ばれると分かる。つまり、割られるのはBADのポジティブ側だと分かる。しかも、割られるのがポジティブ側なら、割った後もポジティブ側だと分かる。
"BAC_p" + "DAC_p" == "BAD_p";
"BAC_p" + "BAC_n" == 360;
"DAC_p" + "DAC_n" == 360;
逆側でも同じだ。
"BCA_p" + "DCA_p" == "BCD_p";
"BCA_p" + "BCA_n" == 360;
"DCA_p" + "DCA_n" == 360;
更に、triangle_lstも、点と繋がっている点が更に別の繋がっている点とも繋がっているかを探していくことで、更新することができるだろう。
ポジティブかネガティブかだが、三角形ならまずポジティブだろう。
triangle_lst := [
"△ABC" : ["BAC_p", "AB", "ABC_p", "BC", "BCA_p", "CA"], #命名のルール、どうしようかなあ
"△ADC" : ["DAC_p", "AD", "ADC_p", "DC", "DCA_p", "CA"]
];
図を見て、取得したい情報が取得できているようなので、これで良いということだろう。
graph := [
"A" : [
[["B"], []],
[["D"], []],
[["C"], []]
]
,
"B" : [
[["A"], []],
[["C"], []]
]
,
"C" : [
[["B"], []],
[["D"], []],
[["A"], []]
]
,
"D" : [
[["A"], []],
[["C"], []]
]
];
"ABC_p" == 168;
"BCD_p" == 108;
"AB" == "BC" == "CD";
"ABC_p" + "ABC_n" == 360;
"BCD_p" + "BCD_n" == 360;
"BAD_p" + "BAD_n" == 360;
"ADC_p" + "ADC_n" == 360;
"BAC_p" + "DAC_p" == "BAD_p";
"BAC_p" + "BAC_n" == 360;
"DAC_p" + "DAC_n" == 360;
"BCA_p" + "DCA_p" == "BCD_p";
"BCA_p" + "BCA_n" == 360;
"DCA_p" + "DCA_n" == 360;
triangle_lst := [
"△ABC" : ["BAC_p", "AB", "ABC_p", "BC", "BCA_p", "CA"], #命名のルール、どうしようかなあ
"△ADC" : ["DAC_p", "AD", "ADC_p", "DC", "DCA_p", "CA"]
];
cluster_lst := [
[["A", "B", "C", "D"], ["BAD_p", "ABC_p", "BCD_p", "ADC_p"]] #ネガティブ同士でもクラスターだと考えるか?いや無いな、辺を追加した時に意味不明になる。
];
BとDを繋ぐ処理も、似たような感じになるだろうから、飛ばす。
次はAとBの辺をその分だけ延長してみる。今回はA側に延長しよう。
もちろんその前に、AとBを繋いだ処理を戻す。それはあの記述法の「記録1」だとかを使えば良いだろう。ここでは省略するが。
まず、graphを更新する。追加する点はEとしよう。
すでにあるBADのネガティブかポジティブを割って、更にBAE・DAEのポジティブ・ネガティブを追加しなければいけない。
今回は、Bがクラスタで、そのクラスタの角はどれもポジティブなので、その場合は必ずネガティブを割ることになるんじゃないかな。
しかも、BAEは180°だな。そうすると、もう一方も必ずポジティブになるな。
"BAE_p" + "DAE_p" == "BAD_n";
"DAE_p" + "DAE_n" == 360;
"BAE_p" == 180;
定義も追加する必要があるな。
"AB" == "AE";
図を見ると、"BAD_p" + "DAE_p" == "BAE_p"、である必要もあるな。しかも、"BAD_p" + "BAE_p" == "DAE_n"、である必要もあるのか。
手元で簡単に、1点から3辺が伸びている図を描いてみると、そういうのが3種類発生するはずだから、これで良いのか。
"BAD_p" + "DAE_p" == "BAE_p";
"BAD_p" + "BAE_p" == "DAE_n";
これは保留だけども、"BAE_n"も追加した方が良いのかなあ。そうすると分かりやすくなる気もするけど。
どういう風な流れで捉えたら良いんだろう。3辺だったらこういうのが3種類発生するのは分かったけど。まあ、いいか。
まあとにかく、既存の角を分割して、新しい角のポジティブネガティブ追加して、3辺だったらこういうのが発生して、という。図を見る限りでは、必要な作業はこれだけだな。
graph := [
"A" : [
[["B"], []],
[["D"], []],
[["E"], []]
]
,
"B" : [
[["A"], []],
[["C"], []]
]
,
"C" : [
[["B"], []],
[["D"], []]
]
,
"D" : [
[["A"], []],
[["C"], []]
]
];
"ABC_p" == 168;
"BCD_p" == 108;
"AB" == "BC" == "CD";
"BAE_p" == 180;
"AB" == "AE";
"ABC_p" + "ABC_n" == 360;
"BCD_p" + "BCD_n" == 360;
"BAD_p" + "BAD_n" == 360;
"ADC_p" + "ADC_n" == 360;
"BAE_p" + "DAE_p" == "BAD_n";
"DAE_p" + "DAE_n" == 360;
"BAD_p" + "DAE_p" == "BAE_p";
"BAD_p" + "BAE_p" == "DAE_n";
triangle_lst := [
];
cluster_lst := [
["BAD_p", "ABC_p", "BCD_p", "ADC_p"] #ネガティブ同士でもクラスターだと考えるか?いや無いな、辺を追加した時に意味不明になる。
];
他の延長も同じだろうから、飛ばす。
じゃあ最初の状態に戻して。次は、垂直二等分線による二等辺三角形の作図。ABを二等分することにしよう。
どの辺に交わるかだけど、今回のクラスタのどれかということなら、ACを作図して角BACと角ABCを比較して、BACの方が大きかったらBCに交わる。BDを作図して角ABDと角BADを比較して、ABDの方が大きかったらADに交わる。そのどちらでも無ければCDに交わる。
graphでACを作成して(クラスタ内なのでポジティブを分割して、それぞれの360°も登録する)、三角形定理ループ(triangle_theorem_loop)を回せば、どちらが大きいかは出るだろう。(その作図を戻すべきかは分からない。とりあえず戻すことにしてみるか。)
BDでも同じ。で、ADに交わると出るかどうか。考えたけど、出るな、△BCDが二等辺三角形で、ABDは132°になる。プログラムとして具体的に考えるなら、「if "ABD_p" > "BAD_p" {~~~} elif ~~~」という具合か。「"BAD_p" + "ADB_p" + 132 == 180」から、「"BAD_p" < 48」を出せれば良いが。
じゃあそういうわけで、ADに点Eを加えて、点Eと点Bを結ぶ。graphをそういう風に更新する(下を参照)。
更に、ADもBも同じクラスタなので、「"ABE_p" + "CBE_p" == "ABC_p"」、「"ABE_p" + "ABE_n" == 360」、「"CBE_p" + "CBE_n" == 360」。
「"AEB_p" + "DEB_p" == "AED_p"」、「"AEB_p" + "AEB_n" == 360」、「"DEB_p" + "DEB_n" == 360」、「"AED_p" == 180」。
定義を追加する。「"AE" == "BE"」。
クラスタを分割したので、cluster_lstに「["B", "C", "D", "E"], ["CBE_p", "BCD_p", "CDE_p", "BED_p"]」も欲しい。A以外で作成すれば良いだろう。
あとはtriangle_lstも更新が必要だろうな。
図を見る限りでは、こんなものだろうか。
graph := [
"A" : [
[["B"], []],
[["D", "E"], []]
]
,
"B" : [
[["A"], []],
[["C"], []],
[["E"], []]
]
,
"C" : [
[["B"], []],
[["D"], []]
]
,
"D" : [
[["A", "E"], []],
[["C"], []]
]
,
"E" : [
[["A"], ["D"]],
[["B"], []]
]
];
"ABC_p" == 168;
"BCD_p" == 108;
"AB" == "BC" == "CD";
"AED_p" == 180;
"AE" == "BE";
"ABC_p" + "ABC_n" == 360;
"BCD_p" + "BCD_n" == 360;
"BAD_p" + "BAD_n" == 360;
"ADC_p" + "ADC_n" == 360;
"ABE_p" + "CBE_p" == "ABC_p";
"ABE_p" + "ABE_n" == 360;
"CBE_p" + "CBE_n" == 360;
"AEB_p" + "DEB_p" == "AED_p";
"AEB_p" + "AEB_n" == 360;
"DEB_p" + "DEB_n" == 360;
triangle_lst := [
"△ABE" : ["BAE", "AB", "ABE", "BE", "AEB", "EA"]
];
cluster_lst := [
[("A", "B", "C", "D"), ["BAD_p", "ABC_p", "BCD_p", "ADC_p"]], #今気付いたが、これは[0]はリストじゃなくて順番が無いから集合だな
[("B", "C", "D", "E"), ["CBE_p", "BCD_p", "CDE_p", "BED_p"]]
];
ADなどでも、特に変わる所は無いだろう。同じ長さの辺を繋がっている辺に落とす、に移る。
じゃあ処理したものを元に戻す。
ABと同じ長さの辺を、BCやADに落とす場合を考えてみる。
まずBCは、角ABCが168°なので、90°以上なので無理だ(参照)。
問題はADだが、まずBからADに垂線を垂らす。具体的には、AD上に点Eを作図して、Bと繋げ、角AEB == 90にする。BもADもクラスタ内なので、処理は前にも見たような感じで。
で、AEとAD/2を比較して、もしAD/2の方が大きければ第2条件はクリア(第1条件は後から)。
更にはAD/2(点Fと名付けよう)と点Bを結んで、BAFとBAEを比較する。BAFの方が大きければ第2条件はクリア。
で、第1条件は角BADが90°以下であることだが、今までの作図を使った方が良いので、こちらを後に持ってくる。今までの作図で確認できなければ、辺AD上の点と、点Bを片っ端から繋げて、何とか確認するべきなのかもしれない。本当は辺BDを繋げれば、角BADは90°以下だと確認できるんだが。
ADの第2条件のBEとBFの作図を具体的にやってみようか。
まず点Eから。上に書いたのを反映する。
ただ一点、点Bにおける3辺の角の和が、ABC_pを割るものだから、例えば"CBE_p" + "ABC_n" == "ABE_n"。その判断をどうするかは分からないけど。
次に点F。大体点Eと同じだろう。
BEと交点は発生し得ないんだが、AD上でのEとの関係が問題にはなる。まあそこも問うているわけだが。あと、角の和やクラスタもより複雑になるか(いやクラスタは同じだった)。
ABE_pとCBE_pのどちらを割っているかが問題だな。もっと言えば、分からない状態でどうするか、そして分かった段階でどう反映するか、だとかが問題だな。
暫定解としては、pやnでは無く、1や2と名付ける、だったか。試してみる。いや、駄目だった。
ABF_? + EBF_p == ABE_?
CBF_? + EBF_p ==CBE_?
新しく区切られた方はどっちもポジティブ。もう片方は必ずどっちもネガティブ(もしクラスタの角がポジティブだったらだけど)。
問題は、ABEやCBEにはもうポジティブやネガティブがあることだ。あの記述法のalwaysで、条件式でポジティブやネガティブを入れるか。というより、制約は本質的にalwaysの所に入れるべきなのかな、その時限りでは無いわけだし。そうなるとあの記述法の意味論の問題になってくるわけだが。いや、うん、やはり制約はalwaysの所に入れるべきだな。
1つの点に4辺ある時、角の和は、隣り合う1+1が4種類、(2)+1が8種類、(3)+1が4種類。1+1+1は、三角形で無く角の和だし、いらないんじゃないかなあ。(3)+1は360°で4種類でもう登録してある。3辺の時は、4辺の時を基準にすると、1+1が1種類、(2)+1が2種類登録してあるわけだ。また、Fの時もEを無視するように同じように1種類と2種類が登録してある。更に、割った時にも割った側の1+1と割ってない側の(2)+1が1種類ずつが登録と。
つまり1+1はEBF_p + 割ってない側 == 割ってない側の点とBとF。
(2)+1は、割ってない側の点とBとFのネガティブ + 割ってない側の角 == EBF_n。割ってない側の点とBとFのネガティブ + EBF_p == 割ってない側の角のネガティブ。割った側の角のネガティブ + 割った側のEBFじゃない方 == EBF_n。割った側の角のネガティブ + EBF_p == 割った側のEBFじゃない方のネガティブ。つまり、EBFについての足し算というか、EBF_nについての2種類と、EBF_pについての2種類かな。
条件は、ABEとABFを比較して、小さいほうが大きい方を割っている。あるいはAEとAFを比較して、小さい方が大きい方を割っている。
if "ABE_p" < "ABF_p" or "AE" < "AF" {
"ABF_n" + "EBF_p" == "ABE_n";
"CBF_p" + "EBF_p" == "CBE_p";
"ABF_n" + "ABE_p" == "EBF_n";
"CBE_n" + "CBF_p" == "EBF_n";
"ABF_n" + "EBF_p" == "ABE_n";
"CBE_n" + "EBF_p" == "CBF_n";
} elif "ABE_p" > "ABF_p" or "AE" > "AF" {
"ABF_p" + "EBF_p" == "ABE_p";
"CBF_n" + "EBF_p" == "CBE_n";
"ABE_n" + "ABF_p" == "EBF_n";
"CBF_n" + "CBE_p" == "EBF_n";
"ABE_n" + "EBF_p" == "ABF_n";
"CBF_n" + "EBF_p" == "CBE_n";
} elif "ABE_p" == "ABF_p" or "AE" == "AF" {
graphの"E"と"F"を統合(今回は"F"を消す)。
"F"が入る三角形とクラスタを消す。
alwaysの式の"F"を"E"に書き換えた上で、被ったものを消す。
この条件式自体を消す。
}
いや、違うな。条件("AE" < "AF"とか)を満たしたら、BADが90°以下かを確認するのか。それ以外の条件を満たした場合は、だからこの作図は無意味で、元に戻して根本的に次の作図に取りかかれば良いのか。
("AE" < "AF")とかに限って、そのままBADが90°以下かの確認に進むかな?しかし、本当に順番はこれで良いのかな。EやFは作図して終わりだと思ってたから、こういう条件による分岐が入ってくると話が違ってきてるんだよな。
人間だったらどうするのかな。点BからAD上の点全部に作図したら話は早いけどね。でも後から戻すとはいえ、その作図は並行した同じステップでやっているわけで、この確認は次のステップに回した方が計算量は少ない気もする。
そうしようかな。だから、条件式前の下の段階で、("AE" < "AF")とかの条件にかけて、当てはまったら作図を元に戻して、点BからAD上へABと同じ長さの辺を作図するということにしようか。
graph := [
"A" : [
[["B"], []],
[["D", "E", "F"], []]
]
,
"B" : [
[["A"], []],
[["C"], []],
[["E"], []],
[["F"], []]
]
,
"C" : [
[["B"], []],
[["D"], []]
]
,
"D" : [
[["A", "E", "F"], []],
[["C"], []]
]
,
"E" : [
[["A"], ["D"]],
[["B"], []],
[["F"], []]
]
,
"F" : [
[["A"], ["D"]],
[["B"], []],
[["E"], []]
]
];
triangle_lst := [
"△ABE" : ["BAE_p", "AB", "ABE_p", "BE", "AEB_p", "EB"],
"△ABF" : ["BAE_p", "AB", "ABF_p", "BF", "AFB_p", "FB"],
"△BEF" : ["EBF_p", "BE", "BEF_p", "EF", "BFE_p", "FB"]
];
cluster_lst := [
[("A", "B", "C", "D"), ["BAD_p", "ABC_p", "BCD_p", "ADC_p"]],
[("B", "C", "D", "E"), ["CBE_p", "BCD_p", "CDE_p", "BED_p"]],
[(""B", "C", "D", "F"), ["CBF_p", "BCD_p", "CDE_p", "BFD_p"]]
];
always {
"ABC_p" == 168;
"BCD_p" == 108;
"AB" == "BC" == "CD";
"AEB_p" == 90;
"AED_p" == 180;
"AF" == "DF";
"AFD_p" == 180;
"ABC_p" + "ABC_n" == 360;
"BCD_p" + "BCD_n" == 360;
"BAD_p" + "BAD_n" == 360;
"ADC_p" + "ADC_n" == 360;
"ABE_p" + "CBE_p" == "ABC_p";
"ABE_p" + "ABE_n" == 360;
"CBE_p" + "CBE_n" == 360;
"AEB_p" + "BED_p" == "AED_p";
"AEB_p" + "AEB_n" == 360;
"BED_p" + "BED_n" == 360;
"BED_p" + "AED_p" == "AEB_n";
"AEB_p" + "AED_p" == "BED_n";
"CBE_p" + "ABC_n" == "ABE_n";
"ABE_p" + "ABC_n" == "CBE_n";
"ABF_p" + "CBF_p" == "ABC_p";
"ABF_p" + "ABF_n" == 360;
"CBF_p" + "CBF_n" == 360;
"AFB_p" + "BFD_p" == "AFD_p";
"AFB_p" + "AFB_n" == 360;
"BFD_p" + "BFD_n" == 360;
"BFD_p" + "AFD_p" == "AFB_n";
"AFB_p" + "AFD_p" == "BFD_n";
"CBF_p" + "ABC_n" == "ABF_n";
"ABF_p" + "ABC_n" == "CBF_n";
}
他の辺も、同じようにできるだろう。
次は、同じ長さの辺の上に、同じ図形を作図する。
ただ、三次元で思い描いた時に、例えばADを重ねるにしても、それを軸に回転できるというか、かなり自由にできることが分かる。
この問題以降の問題も見てみて考えるに、これはクラスタとクラスタを合わせてクラスタを拡大するということじゃないかと思うので、暫定的にそういうことにする。
そうすると、四角形だけじゃなく三角形も、五角形も、何角形だろうが、クラスタとして扱わなければならないのではないか。
そして、クラスタを同じ方向に重ね合わせて、交点を確認するというのは、不毛なのではないか。
だとしたら、絶対に三角形が発生することは無いので、1ステップでは無駄だ。しかし、試しにそのクラスタの拡大だけはやってみよう。
ABとBCを重ねてみよう。元CをE、元DをFとする。
[["B", "C", "E", "F"], ["CBF_p", "BC", "BCE_p", "CE", "CEF_p", "EF", "BFE_p", "FB"]]
"BCE_p" == 168;
"CEF_p" == 108;
"BC" == "CE" == "EF";
"BCE_p" + "BCE_n" == 360;
"CEF_p" + "CEF_n" == 360;
"CBF_p" + "CBF_n" == 360;
"BFE_p" + "BFE_n" == 360;
で、こうしたい。
[["A", "B", "F", "E", "C", "D"], ["BAD_p", "AB", "ABF_?", "BF", "BFE_p", "EF", "CEF_p", "CE", "DCE_?", "CD", "ADC_p", "AD"]
ABC_p + CBF_p == ABF_?
BCD_p + BCE_p == DCE_?
["A", "B", "C", "D"]と["B", "C", "E", "F"]だが、後者は["C", "E", "F", "B"]でもあって、これをひっくり返すと["B", "F", "E", "C"]。それをそのまま挿入してこの結果になる。つなぎ目のBとCの角は、足し算で記述する必要がある、がポジティブかネガティブかが確実に分かるわけでは無い。
EとFは新しい点なので、今度こそ「ABF_1」とかで良いのかもしれない。
…そもそも、クラスタで考えず「ABC_p + CBF_p == ABF_1」じゃ駄目なのかな。3Dでそのルールを守りながら違う図を描けるから駄目なのか。
で、alwaysでif文を作って、満たし次第その条件文は消去することにするか。
このクラスタ、面なんじゃないかな。