sasaharayuugo.net

ジュニア算数オリンピック　二次元上のユークリッド幾何の問題　その２５

ジュニア算数オリンピックにおけるユークリッド幾何学の問題の解答の自動化を模索している。まず三角形定理ループを回し、回答できなかったら1ステップの作図を試していって、それらで回答できるか探る。それでも駄目だったら2ステップ、3ステップと増やしていく。交点の確認はこの方法を使う。
　

　

06年度トライアル問題　問題9

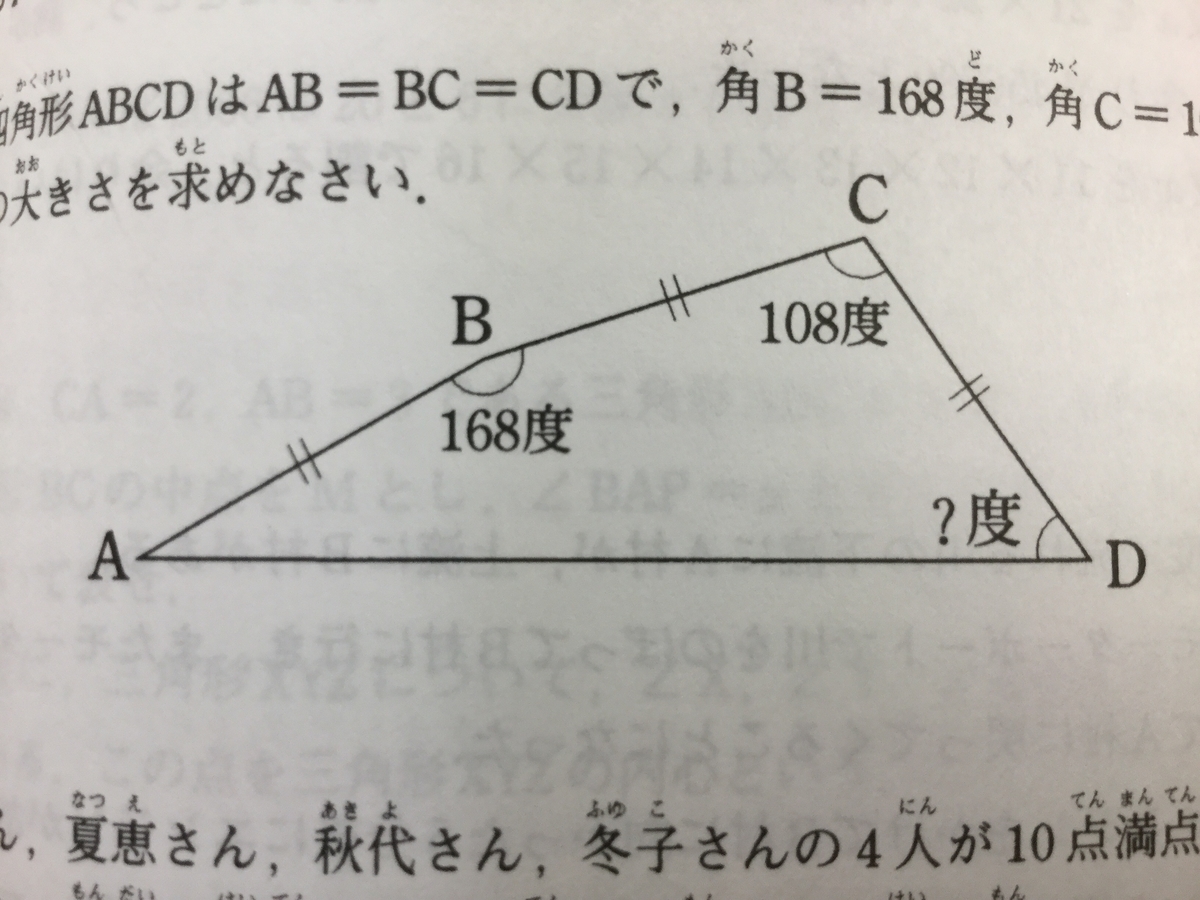
『図の四角形ABCDはAB＝BC＝CDで、角B＝168度、角C＝108度です。角Dの大きさを求めなさい。

』


では初期条件。

graph := [
        A : [
            [[B], []],
            [[D], []]
        ]
        ,
        B : [
            [[A], []],
            [[C], []]
        ]
        ,
        C : [
            [[B], []],
            [[D], []]
        ]
        ,
        D : [
            [[A], []],
            [[C], []]
        ]
    ];

    parallel_lines_lst := [
    ];

    triangle_lst := [
    ];

    always {
        ABC_p == 168;
        BCD_p == 108;
        AB == BC == CD;
    }


辺による辺の和も180°の角の和も無し。平行線も無し。graphを辿っても三角形は見つからない。前回説明した方法での角の和の登録も、使う必要無し。

作図

セットアップが終わったので、作図に移る。
セットアップ時の角の和の取得法について - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その２１ - ニート歴10年からの数学日記の後半、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その１８ - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その１７ - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その１６ - ニート歴10年からの数学日記、
辺りを参考にしようかな、後ろに行くほどもう参考にならないと思うけど。


まず点と点を結ぶ所から。

graphの最初のAを確認して、graphの繋がっていないCと単純に繋げる。

graph := [
        A : [
            [[B], []],
            [[D], []],
            [[C], []]
        ]
        ,
        B : [
            [[A], []],
            [[C], []]
        ]
        ,
        C : [
            [[B], []],
            [[D], []],
            [[A], []]
        ]
        ,
        D : [
            [[A], []],
            [[C], []]
        ]
    ];


交点を判断するのに三角関数を使うなら、実はこの段階でもう答えは分かってしまう。ACの（CDと比べた時の）長さは分かるし、角ACDも分かるし、それで角ADCも分かってしまう（いや、ACDはBCDの角の和が分からないと計算できないか）。


まあ流れとしては、セットアップ時の角の和の取得法について - ニート歴10年からの数学日記の後半で書いたようなことを、順番なんか適当で、乱れ打ちでやってしまう。

交点の発見は、作図されたACに繋がっている辺と辺で、片っ端から三角関数にかけていく。更にはACに繋がった辺を基準に、ACと他の辺で三角関数にかけていく。
おそらくそういう風になるだろう。

交点が発生したら、その交点について最初にやるみたいに、辺の和だとかを登録していく。
更に、角だとか辺の大きさが明らかになるたびに、その角や辺について同じように片っ端から三角関数にかけていく。今は計算量のことは何も考えていない。

なんかそれぐらいのラフさでゴールまで行ける気がする。作図後の角の和については、まだ問題があるが。
最適化については、この程度の計算量なら、動いた後に考えれば良い。

もしクラスタがあれば、AとCを繋げた時に、角の和を登録できるんだがな。このままでは、Bを基準に考えたとしても、例えばDが今とは反対側にあるという場合もあり得るんじゃないか。辺と辺の繋がりでは無く、中の面で捉える必要があるのではないか。そうでなければ角の和は登録できないのではないか。


ちょっと今日は寝不足なのか、調子が悪い。

よく考えたら、三角関数は、辺がZのように繋がっている時はどうなるのだろう。点と点の間でも、辺の並びは時計回りとかで統一した方が良いのだろうか。ある辺から、左回りと右回りでポジティブな角同士の時だけに、三角関数を適用すべきなのだろうか。

それならできるような気もするが、分からん。

どうなんだろうと思ったが、平行線リストの亜種みたいなものなのかもしれない。3点が平面上にあって、1辺を基準にした2種類の最大のポジティブの角で、時計回りと反時計周りだったら、三角関数の対象になる。


交点を判定して、その後に発生する角の和も180°の角の和なんで簡単なんで良いとして、問題は点に辺を付け加える時の角の和の更新だろう。

その付け加える辺がAB、元々あった辺をACとして、辺AB上の点がACと繋がっていたら、時計回りとかを利用すれば2辺の位置関係は分かるのではないか。
例えば、普通にAとBがCと繋がっているとして、Cが左にあったらCにおいてA, Bの順番だし、Cが右にあったらB, Aだ。

2辺の関係が分かれば、何と何の間なのかは分かるだろう。他に方法ってあるのかな。


ただ、辺において点の位置が不確定なことがあったように、点においても辺と辺の位置が不確定なことがあるはずで、それに対応することを考えると面倒くさい。
二つの形式を考えた。

C : [
        F : [[], [], [B, H, G, D]],
        B : [[F], [], [H, G, D]],
        H : [[F, B], [], [G, D]],
        G : [[F, B, H], [], [D]],
        D : [[F, B, H, G], [], []]
    ]

    C : [
        [[], F, [], [B, H, G, D]],
        [[F], B, [], [H, G, D]],
        [[F, B], H, [], [G, D]],
        [[F, B, H], G, [], [D]],
        [[F, B, H, G], D, [], []]
    ]

まあどっちでも良いんだけども。こういうの、必要なんじゃないのかな。
自分で書くのが面倒くさい場合は、内部でテキストというか形式を生成して使っても良いかもしれない。そういう風に考えれば良いんじゃないのかな。


作図自体は問題にはならないだろう、多分（いや、作図の時に角の和だけは割っておく必要があるのかな？）。今日はここで終わりにしておく。