08年度ファイナル問題 問題12
『(せめて画像だけにしようと思っていたのだけど、ちょっとサイズ的に。二回書くのも何なので問題文は省略)
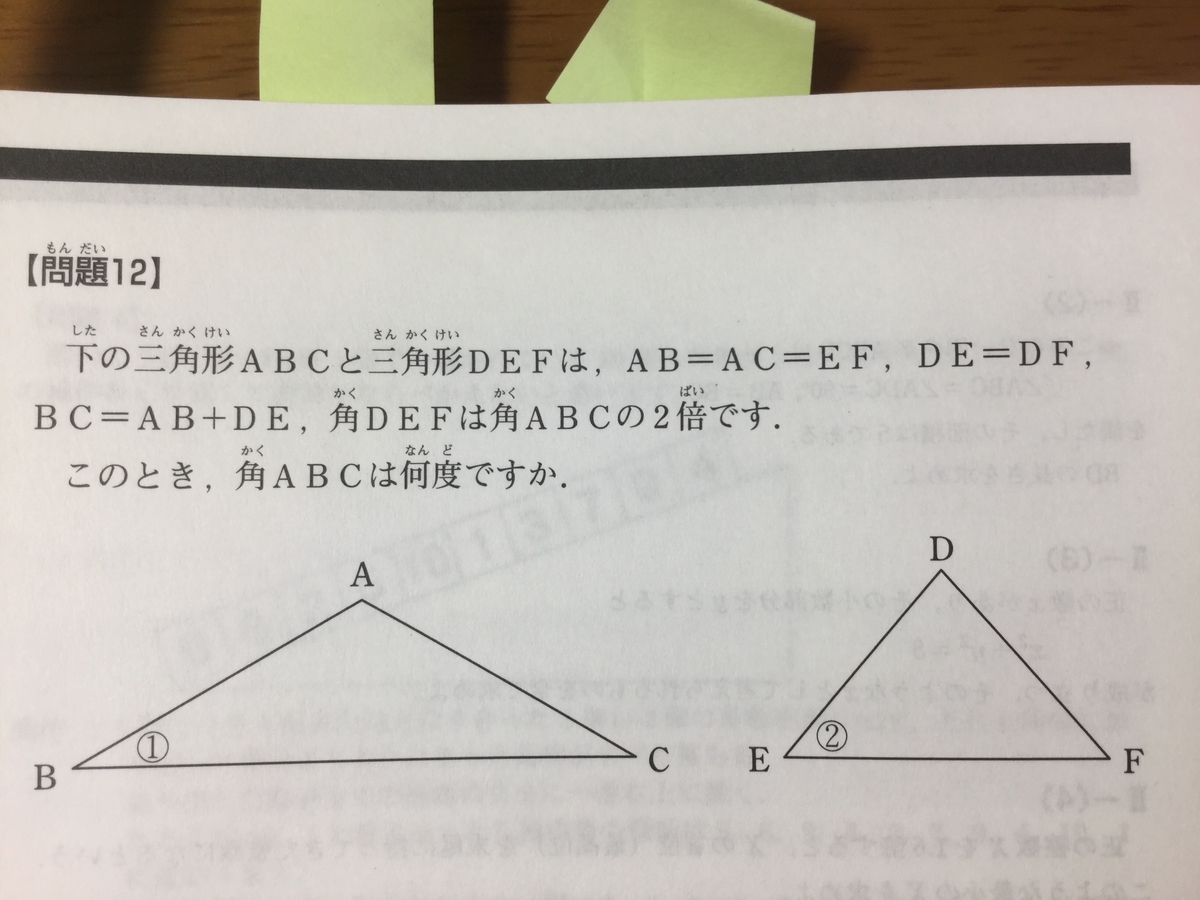 』
』
今回は2つあるわけだけど、大丈夫かな。では初期条件。
graph := [
A : [
[[B], [], []],
[[C], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []]
]
,
C : [
[[A], [], []],
[[B], [], []]
]
,
D : [
[[E], [], []],
[[F], [], []]
]
,
E : [
[[D], [], []],
[[F], [], []]
]
,
F : [
[[D], [], []],
[[E], [], []]
]
];
clockwise_lst := [
A : [
[C, [], [], [B]],
[B, [C], [], []],
~
]
,
B : [
[A, [], [], [C]],
[C, [A], [], []],
~
]
,
C : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
,
D : [
[F, [], [], [E]],
[E, [F], [], []],
~
]
,
E : [
[D, [], [], [F]],
[F, [D], [], []],
~
]
,
F : [
[E, [], [], [D]],
[D, [E], [], []],
~
]
];
angle_lst := [
A : [
[
[C, [], [], [B]],
[B, [C], [], []]
]
]
,
B : [
[
[A, [], [], [C]],
[C, [A], [], []]
]
]
,
C : [
[
[B, [], [], [A]],
[A, [B], [], []]
]
]
,
D : [
[
[F, [], [], [E]],
[E, [F], [], []]
]
]
,
E : [
[
[D, [], [], [F]],
[F, [D], [], []]
]
]
,
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C],
[D, E, F]
];
triangle_lst := [
];
cluster_lst := [
];
always {
AB == AC == EF;
DE == DF;
BC == AB + DE;
DEF_p == ABC_p * 2;
}
辺による辺の和も180°の角の和も無し。angle_lstによる角の和も無し。平行線も無し。
graphを辿って、△ABCと△DEF。clusterも更新。
graph := [
A : [
[[B], [], []],
[[C], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []]
]
,
C : [
[[A], [], []],
[[B], [], []]
]
,
D : [
[[E], [], []],
[[F], [], []]
]
,
E : [
[[D], [], []],
[[F], [], []]
]
,
F : [
[[D], [], []],
[[E], [], []]
]
];
clockwise_lst := [
A : [
[C, [], [], [B]],
[B, [C], [], []],
~
]
,
B : [
[A, [], [], [C]],
[C, [A], [], []],
~
]
,
C : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
,
D : [
[F, [], [], [E]],
[E, [F], [], []],
~
]
,
E : [
[D, [], [], [F]],
[F, [D], [], []],
~
]
,
F : [
[E, [], [], [D]],
[D, [E], [], []],
~
]
];
angle_lst := [
A : [
[
[C, [], [], [B]],
[B, [C], [], []]
]
]
,
B : [
[
[A, [], [], [C]],
[C, [A], [], []]
]
]
,
C : [
[
[B, [], [], [A]],
[A, [B], [], []]
]
]
,
D : [
[
[F, [], [], [E]],
[E, [F], [], []]
]
]
,
E : [
[
[D, [], [], [F]],
[F, [D], [], []]
]
]
,
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C],
[D, E, F]
];
triangle_lst := [
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△DEF : [EDF_p, DE, DEF_p, EF, DFE_p, EF]
];
cluster_lst := [
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[D, E, F], [EDF_p, DE, DEF_p, EF, DFE_p, EF]]
];
always {
AB == AC == EF;
DE == DF;
BC == AB + DE;
DEF_p == ABC_p * 2;
}
作図
セットアップが終わったので、作図に移る。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その26 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その25 - ニート歴10年からの数学日記、
セットアップ時の角の和の取得法について - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その21 - ニート歴10年からの数学日記の後半、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その18 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その17 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その16 - ニート歴10年からの数学日記、
辺りを参考にしようかな、後ろに行くほどもう参考にならないと思うけど。
- 点と点を結ぶ
- 線を同じ分だけ延長する
- 二等辺三角形の作図1
- 二等辺三角形の作図2
- クラスタを貼り合わせる
- 正三角形の作図(必要だと分かった)
- ?正四角形の判定
- ?正五角形の判定
まず点と点を結ぶ所から。手順に慣れるために、前回と同じでも繰り返そうと思う。
って、繋がってない点と点が今は無いのか。
じゃあ次、線を同じ分だけ延長。
graphのAの一番最初のBの反対側に、Gを追加しよう。
AB == AG。かつangle関係も更新する。平面リストにも追加する必要があるんだな。
angle_lstでは、AにおいてBが端っこにある角があれば、その反対側に追加する。角の間にある場合は、つまり角が全部で180°を超えるということになるので、新しく作成を模索する必要があるが、今回は無い。
graph := [
A : [
[[B], [], [G]],
[[C], [], []]
]
,
B : [
[[A, G], [], []],
[[C], [], []]
]
,
C : [
[[A], [], []],
[[B], [], []]
]
,
D : [
[[E], [], []],
[[F], [], []]
]
,
E : [
[[D], [], []],
[[F], [], []]
]
,
F : [
[[D], [], []],
[[E], [], []]
]
,
G : [
[[A, B], [], []]
]
];
clockwise_lst := [
A : [
[G, [], [], [C, B]]
[C, [G], [], [B]],
[B, [C, G], [], []],
~
]
,
B : [
[A, [], [], [C]],
[C, [A], [], []],
~
]
,
C : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
,
D : [
[F, [], [], [E]],
[E, [F], [], []],
~
]
,
E : [
[D, [], [], [F]],
[F, [D], [], []],
~
]
,
F : [
[E, [], [], [D]],
[D, [E], [], []],
~
]
,
G : [
[A, [], [], []],
~
]
];
angle_lst := [
A : [
[
[G, [], [], [C, B]]
[C, [G], [], [B]],
[B, [C, G], [], []]
]
]
,
B : [
[
[A, [], [], [C]],
[C, [A], [], []]
]
]
,
C : [
[
[B, [], [], [A]],
[A, [B], [], []]
]
]
,
D : [
[
[F, [], [], [E]],
[E, [F], [], []]
]
]
,
E : [
[
[D, [], [], [F]],
[F, [D], [], []]
]
]
,
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
,
G : [
[
[A, [], [], []]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C, G],
[D, E, F]
];
triangle_lst := [
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△DEF : [EDF_p, DE, DEF_p, EF, DFE_p, EF]
];
cluster_lst := [
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[D, E, F], [EDF_p, DE, DEF_p, EF, DFE_p, EF]]
];
always {
AB == AC == EF;
DE == DF;
BC == AB + DE;
DEF_p == ABC_p * 2;
AB == AG;
}
graphから辺の和と180度の角の和を取得。
AB + AG == BG;
BAC_p + CAG_p == BAG_h;
angle_lstから角の和を取得。
CAG_p + BAC_p == BAG_h; #あー、180度の時ってどうしよう
交点はACを基準に調べることになるだろう。angle_lstのAにおいてGはCの上にある。しかしangle_lstのCにおいてAの下には何も無い。なので、ACを基準に三角関数で調べられるような辺のセットは無いと分かる。
やることと言えば、最初の手順みたいなのと、交点の発見と、辺や角において順番が不確定なものの確定と、ぐらいだっけか?(セットアップ時の角の和の取得法について - ニート歴10年からの数学日記の後半参照)
じゃあとりあえず結果を表示して次の作図に行こうか。
graph := [
A : [
[[B], [], [G]],
[[C], [], []]
]
,
B : [
[[A, G], [], []],
[[C], [], []]
]
,
C : [
[[A], [], []],
[[B], [], []]
]
,
D : [
[[E], [], []],
[[F], [], []]
]
,
E : [
[[D], [], []],
[[F], [], []]
]
,
F : [
[[D], [], []],
[[E], [], []]
]
,
G : [
[[A, B], [], []]
]
];
clockwise_lst := [
A : [
[G, [], [], [C, B]]
[C, [G], [], [B]],
[B, [C, G], [], []],
~
]
,
B : [
[A, [], [], [C]],
[C, [A], [], []],
~
]
,
C : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
,
D : [
[F, [], [], [E]],
[E, [F], [], []],
~
]
,
E : [
[D, [], [], [F]],
[F, [D], [], []],
~
]
,
F : [
[E, [], [], [D]],
[D, [E], [], []],
~
]
,
G : [
[A, [], [], []],
~
]
];
angle_lst := [
A : [
[
[G, [], [], [C, B]]
[C, [G], [], [B]],
[B, [C, G], [], []]
]
]
,
B : [
[
[A, [], [], [C]],
[C, [A], [], []]
]
]
,
C : [
[
[B, [], [], [A]],
[A, [B], [], []]
]
]
,
D : [
[
[F, [], [], [E]],
[E, [F], [], []]
]
]
,
E : [
[
[D, [], [], [F]],
[F, [D], [], []]
]
]
,
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
,
G : [
[
[A, [], [], []]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C, G],
[D, E, F]
];
triangle_lst := [
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△DEF : [EDF_p, DE, DEF_p, EF, DFE_p, EF]
];
cluster_lst := [
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[D, E, F], [EDF_p, DE, DEF_p, EF, DFE_p, EF]]
];
always {
AB == AC == EF;
DE == DF;
BC == AB + DE;
DEF_p == ABC_p * 2;
AB == AG;
AB + AG == BG;
BAC_p + CAG_p == BAG_h;
}
じゃあリセットして次の種類の作図。
次の作図は二等辺三角形の作図で、三角形の内部でのみ作ることにしていて、二種類ともどちらの辺と作るかは角度で決めているのだけど、しかし角度がイコールな場合はどちらの作図もできないんだな。新しい発見だった。
あー、一番最初に三角形定理ループを回すのを忘れてるな。まあ良いか。
いや待てよ。話は戻るが、一番最初の作図は、例えばAとDを結んだりもできたんじゃないか?
いや、でも理想としてはやりたくないんだよな。というのも、全然違う空間にある三角形同士なのだし。
同一平面上にある点同士に限るのは極端だろうか。しかし辺を辿って繋がっている点を保持するリストなんて余計なものは、作りたく無いしなあ。
まあ今回は、考察自体を保留としようかな。できれば省きたいんだが、どうやって省くかというのは。
じゃあ次、リセットしてから、クラスタの接続。クラスタの同じ長さの辺を繋ぐ。
今回はABかACにEFを繋ぐ。どっちにどう繋いでも、それで答えまで行くはずだが。
cluster_lst := [
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[D, E, F], [EDF_p, DE, DEF_p, EF, DFE_p, EF]]
];三角形ABCのABに、複製したDEFのEFを繋ぐことにしよう。AにEを、BにFを対応させる。複製した元々Dだった点は、Gと名付けることにしよう。
と思ったのだけど、時計回りを保持したほうが良いのが分かったので、AにFを、BにEを対応させることにした。
[[G, B, A], [AGB_p, BG, ABG_p, AB, BAG_p, AG]]
EDF_p == AGB_p;
DE == BG;
DEF_p == ABG_p;
EF == AB;
DFE_p == BAG_p;
EF == AG;
という感じにしたい。
angle_lstについて、とりあえずはこの上が下になるはず。
D : [
[
[F, [], [], [E]],
[E, [F], [], []]
]
]
,
E : [
[
[D, [], [], [F]],
[F, [D], [], []]
]
]
,
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
G : [
[
[A, [], [], [B]],
[B, [A], [], []]
]
]
,
B : [
[
[G, [], [], [A]],
[A, [G], [], []]
]
]
,
A : [
[
[B, [], [], [G]],
[G, [B], [], []]
]
]
それで、繋げた角が180°以下だと判定される前はこう。
graph := [
A : [
[[B], [], []],
[[C], [], []],
[[G], [], []]
]
,
B : [
[[G], [], []],
[[A], [], []],
[[C], [], []]
]
,
C : [
[[A], [], []],
[[B], [], []]
]
,
D : [
[[E], [], []],
[[F], [], []]
]
,
E : [
[[D], [], []],
[[F], [], []]
]
,
F : [
[[D], [], []],
[[E], [], []]
]
,
G : [
[[A], [], []],
[[B], [], []]
]
];
clockwise_lst := [
A : [
[C, [], [], [B, G]],
[B, [C], [], [G]],
[G, [B, C], [], []]
~
]
,
B : [
[G, [], [], [A, C]],
[A, [G], [], [C]],
[C, [A, G], [], []],
~
]
,
C : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
,
D : [
[F, [], [], [E]],
[E, [F], [], []],
~
]
,
E : [
[D, [], [], [F]],
[F, [D], [], []],
~
]
,
F : [
[E, [], [], [D]],
[D, [E], [], []],
~
]
,
G : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
];
angle_lst := [
A : [
[
[C, [], [], [B]],
[B, [C], [], []]
]
,
[
[B, [], [], [G]],
[G, [B], [], []]
]
]
,
B : [
[
[A, [], [], [C]],
[C, [A], [], []]
]
,
[
[G, [], [], [A]],
[A, [G], [], []]
]
]
,
C : [
[
[B, [], [], [A]],
[A, [B], [], []]
]
]
,
D : [
[
[F, [], [], [E]],
[E, [F], [], []]
]
]
,
E : [
[
[D, [], [], [F]],
[F, [D], [], []]
]
]
,
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
,
G : [
[
[A, [], [], [B]],
[B, [A], [], []]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C, G],
[D, E, F]
];
triangle_lst := [
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△DEF : [EDF_p, DE, DEF_p, EF, DFE_p, EF]
];
cluster_lst := [
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[D, E, F], [EDF_p, DE, DEF_p, EF, DFE_p, EF]],
[[G, B, A], [AGB_p, BG, ABG_p, AB, BAG_p, AG]]
];
always {
AB == AC == EF;
DE == DF;
BC == AB + DE;
DEF_p == ABC_p * 2;
EDF_p == AGB_p;
DE == BG;
DEF_p == ABG_p;
EF == AB;
DFE_p == BAG_p;
EF == AG;
}
で、どちらも180°以下(一方はちょうど180°)なので、こうなる。
結果的に、graphをAのを直線に直した、angle_lstを統合した、クラスタを追加した。
いや、ああでも、Eの角は同じ大きさのが2つあるから90°以下で、だからその半分が加わっても180°以下か。結構しっかりした以上以下の演算が必要で、だからやっぱり自動化は無理なんだろうな。三角関数の関数はあるだろうから、良さそうなソルバー(制約プログラミング言語では無い純粋な解答プログラム)さえ見つかれば、自動化できるのかもしれないけど。
graph := [
A : [
[[B], [], []],
[[C], [], [G]]
]
,
B : [
[[G], [], []]
[[A], [], []],
[[C], [], []]
]
,
C : [
[[A], [], []],
[[B], [], []]
]
,
D : [
[[E], [], []],
[[F], [], []]
]
,
E : [
[[D], [], []],
[[F], [], []]
]
,
F : [
[[D], [], []],
[[E], [], []]
]
,
G : [
[[A], [], []],
[[B], [], []]
]
];
clockwise_lst := [
A : [
[C, [], [], [B, G]],
[B, [C], [], [G]],
[G, [B, C], [], []]
~
]
,
B : [
[G, [], [], [A, C]],
[A, [G], [], [C]],
[C, [A, G], [], []],
~
]
,
C : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
,
D : [
[F, [], [], [E]],
[E, [F], [], []],
~
]
,
E : [
[D, [], [], [F]],
[F, [D], [], []],
~
]
,
F : [
[E, [], [], [D]],
[D, [E], [], []],
~
]
,
G : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
];
angle_lst := [
A : [
[
[C, [], [], [B, G]],
[B, [C], [], [G]],
[G, [B, C], [], []]
]
]
,
B : [
[
[G, [], [], [A, C]],
[A, [G], [], [C]],
[C, [A, G], [], []]
]
]
,
C : [
[
[B, [], [], [A]],
[A, [B], [], []]
]
]
,
D : [
[
[F, [], [], [E]],
[E, [F], [], []]
]
]
,
E : [
[
[D, [], [], [F]],
[F, [D], [], []]
]
]
,
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
,
G : [
[
[A, [], [], [B]],
[B, [A], [], []]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C, G],
[D, E, F]
];
triangle_lst := [
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△DEF : [EDF_p, DE, DEF_p, EF, DFE_p, EF]
];
cluster_lst := [
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[D, E, F], [EDF_p, DE, DEF_p, EF, DFE_p, EF]],
[[G, B, A], [AGB_p, BG, ABG_p, AB, BAG_p, AG]],
[[A, G, B, C], [CAG_p, AG, AGB_p, BG, CBG_p, BC, ACB_p, AC]]
];
always {
AB == AC == EF;
DE == DF;
BC == AB + DE;
DEF_p == ABC_p * 2;
EDF_p == AGB_p;
DE == BG;
DEF_p == ABG_p;
EF == AB;
DFE_p == BAG_p;
EF == AG;
}
よく分からないけど、これで答えまで行くはずなんだけど。こんなんで良いのかな。次回はまた別の問題で可能か探ってみるけど。