まず、統語法則とは何か。統語法則とは「バラバラな⾔葉たちを、1つのまとまった意味にする法則」のことだ。
統語法則の内の「単語を⽂にまとめる法則」ということであれば、⾃然⾔語(プログラミング⾔語などに対して⽇本語や英語などのこと)においては、原理的には主要部先導型と主要部終端型の⼤きく⼆種類がある。
⽊構造は、ただ何が何を含んでいるかを表しているという意味で、学校で習うような集合論を線によって表したものでしか無い。⾔い換えれば、単語から⽂へのまとまりは、このような形で集合論によって記述され得る。

※この英語の図では動詞が主語を含んでいて、また「bug」が「a」を含んでいると解釈されているが、「主語が動詞を含んでいて、またaがbugを含んでいる」と解釈するのも意味的には可能な⽂だ。発⾒したのが彼なのか、彼が発⾒したのか、これはどちらなのかは分からない。私は後者の解釈を採⽤している。「monstrous verminous bug」は⼀語として認識されていると解釈している。
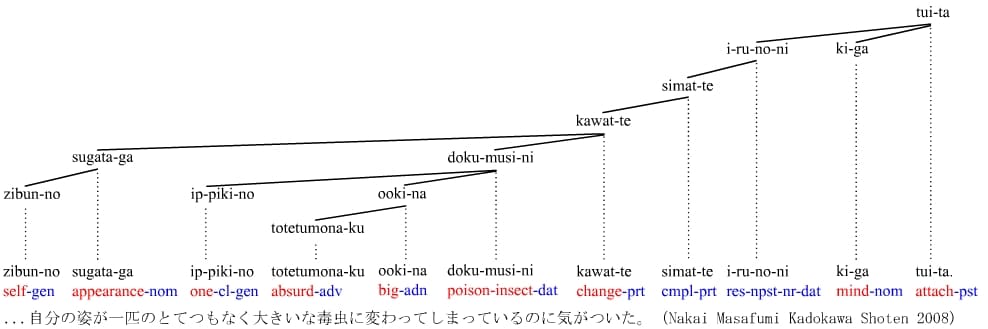
※wikipedia「主要部」(https://ja.wikipedia.org/wiki/%E4%B8%BB%E8%A6%81%E9%83%A8)から引⽤。
細部から全体の順番で記述する主要部終端型⾔語は、ひどく奇妙なものにも⾒える。ここでは主要部終端型⾔語に対して、もう1つの解釈を提⽰しておきたい。
ここでタイトルにあった「フローチャート」が出てくる。ここで⾔う「フローチャート」とは、前提があって選択肢があって結果があるような、要するに⽇常で使うようなフローチャートのことだ。
フローチャートの例えば「条件」や「選択肢」などの概念は、⾃然⾔語においては集合論の概念と同じくらいに重要なものだし、実際同じくらいの⾼い頻度で出てくる。
だからというわけでは無いが、私の研究では、集合論とは別の論理体系としてフローチャートも重視している。
「必要条件」という、集合論ともフローチャートともつかない概念がある。「必要条件」をデジタル⼤辞泉で調べると
ある事柄が成⽴するために必要な条件。命題「AならばB」が成り⽴つとき、BはAの必要条件という。
と書いてあるが、「必要」や「条件」はフローチャートの概念でもある。実はこの地点で集合論とフローチャートは交わっている。
フローチャートにおいては、前提から結果に繋がった時に、その結果から前提を振り返ると、結果は前提を内包しているかのようになる。もっとハッキリ⾔えば、その時にフローチャートはまとまっているかのようになる。
もちろん「必要条件」は集合論の概念でしか無い。しかし例えば辞書において、集合論の概念を集合論以外で説明する時に使われるぐらいには、この時フローチャートは集合論と似たような振る舞いをする。
主要部終端型⾔語も、この原理で説明できないだろうか。
つまり1つ⽬の単語からフローチャートで繋がっていって、最後の単語に到着した時に、まるで最後の単語がそれまでの単語を含んでいたかのようになって、あの奇妙な⽊構造を形作る。
これは仮説でしか無いし、これからの⽂章もこの仮説無しで読めるようになっている。しかしこの仮説が本当であれば、単語から⽂への統語法則にも部分的にフローチャートが絡んでいることになる。
⽇本語は主要部終端型⾔語なので、後ろの単語が前の単語を集合論的に含む。ただしかし、読点によって区切られているブロックが、必ずしも1つの集合としてまとまっているとは限らない。
例えば「AだったりBだったり、Cだったりするかもしれない。」という⽂を考えてみると、「Aだったり」と「Bだったり」は「Cだったり」と意味的に並列で、別に「Bだったり」が「Aだったり」を集合論的に含んでいるわけでは無い。
しかし、区切られている以上はその区切りの中に、1つだろうが並⾏した2つだろうが、まとまった集合が存在しているのは確かだ。その点で、主要部終端型⾔語だという意識は読点の打ち⽅への理解を助ける。
次のページからは、主に集合論とフローチャートを使って、⽇本語における⼦⾳と⺟⾳の意味を記述している。この理論と主要部終端型⾔語だというのを組み合わせることで、より詳細に読点の集合論的なまとまりを把握できるようになる。
2018年11月の論文(https://sasaharayuugo.net/kurorekishi/facebook1-tumblr-facebook2/2018-11-facebook.html)を掲載。
「脱ニート前に考えたこと」の「文章の制約」(https://sasaharayuugo.net/kurorekishi/datsuNeet/10-23-1651.html)を掲載。