03年度ファイナル問題 問題2
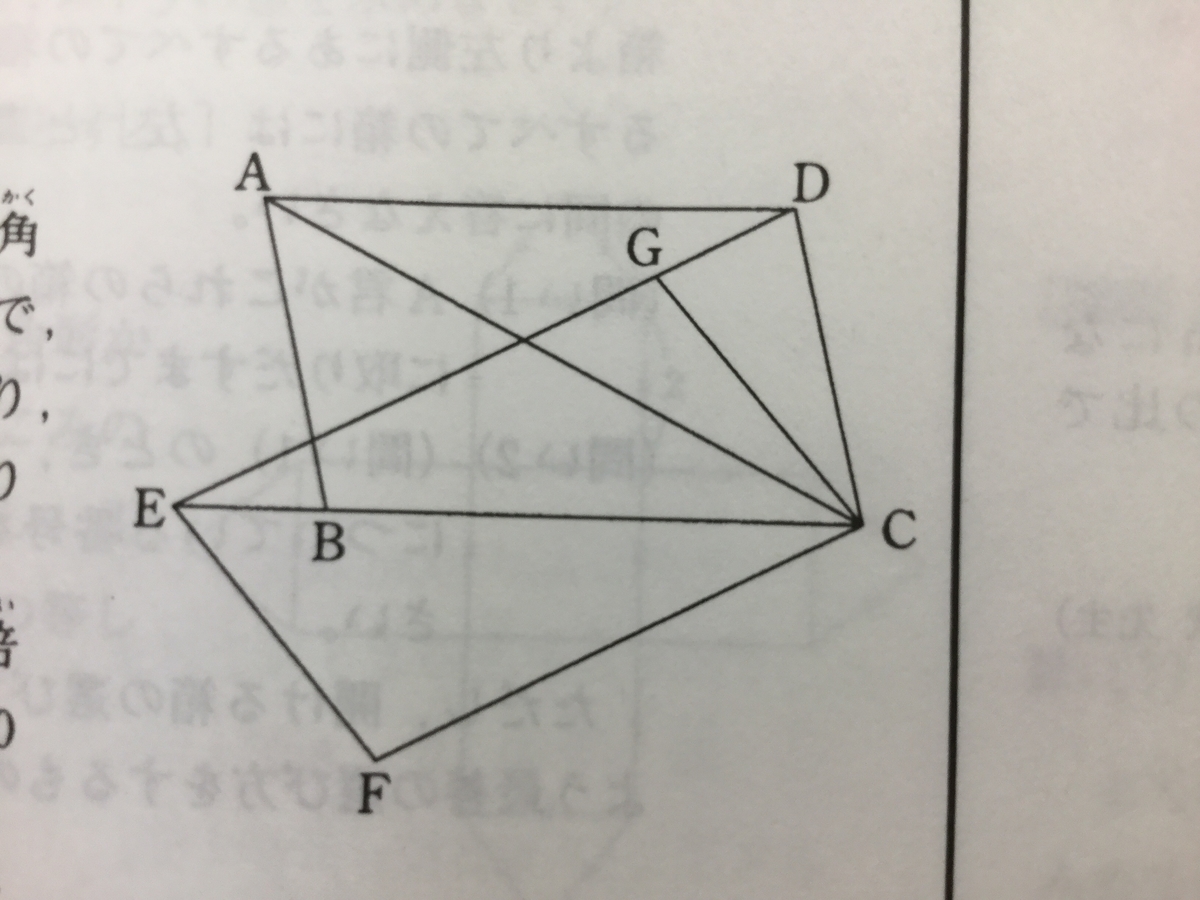
『右の図の四角形ABCDと四角形EFCGは合同な平行四辺形で、辺EGを延長した線は点Dを通り、辺CBを延長した線は点Eを通ります。
このとき、角BACの[ア]倍と角CADの[イ]倍の和は180度となります。
[ア]、[イ]に入る整数をそれぞれ答えなさい。
 』
』
今回で2回目になるが、この問題は自分には予想外だった。具体的な数値が出ないので、並び替えできない。
ではまず、平行線と三角形の種類を確認する。いや、その前に、交点を上から、H、Iと名付けておく。
平行線は、ADとEC、ADとEB、ADとBC。EDとFC、EGとFC、IDとFC、EHとFC、IGとFC、HDとFC、EIとFC、IHとFC、HGとFC、GDとFC。
同位角や錯角を探す上で、この処理は結構重要ではないか。直線で結ばれているものだけ入れれば良いのかもしれないが。
三角形はどう探そうかな。点Aから、繋がっている点を探して、その点と三角形になってないか調べるか、とりあえず。
AはBとCとDに結び付いている。ABと来て、BはCとも結び付いているので、ABC。BはDとは結び付いていない。ACと来て、CはDと結び付いているので、ACD。こういう感じで探していこうかな。
CDE、CDG、CDH、CEG、CEH、CGH。これだけだった。
平行線は、ADとEC、ADとEB、ADとBC。EDとFC、EGとFC、IDとFC、EHとFC、IGとFC、HDとFC、EIとFC、IHとFC、HGとFC、GDとFC。
三角形は、ABC、ACD、CDE、CDG、CDH、CEG、CEH、CGH。
以後、何かが作図されるたびに確認していく(あるいは作図のフェーズが終わって公理のフェーズに入る時か)。まあいつか、必要無いと分かったらこの処理はできる範囲で縮小したいと思う。
ちょっと昨日は最初に飛ばしすぎて疲れたので、早めに休憩しよう。
では平行線の同位角・錯角から確認していく。
まずADとECから。∠ACE=∠CAD、∠ADE=∠CED。∠ADE=∠DEB、∠DAB=∠ABE。で、ADとBCで探し始めて気付いたわけだけど、平行線の一方の端ともう一方の逆側の端がそれぞれ結び付いていないと、錯角を確認する必要は無いみたいだ。それなら、そもそも最初のステップで追加する平行線のセットも減らせる。同位角はセットでは無く辺に着目すれば良い。
EDとFC以下は、錯角の登録の必要は無し。いや違うな、そもそも、大きな並行線を見つけて、その間の線の単位で探していけば、錯角も同位角も見つかるのか。馬鹿だったな、本当にね。錯角あったわ。
ああちょっとやりなおそう。休憩。
大きな平行線に注目したとして、ADとECだと、AB・AC・DE・DCで繋がっている。
ABに注目すると、∠DAB=∠ABE。ACに注目すると、∠DAC=∠ACB、∠DAC=∠ACE。DEに注目すると、∠ADE=∠DEB、∠ADE=∠DEC。DCは無し。
大きな平行線、EDとFCに注目するとして、EF・EC・HC・GC・DCで繋がっている。一方の線の点を一つずつ確認していけば良いみたいだ。
EFに注目すると、無し。ECに注目すると、∠DEC=∠ECF、∠GEC=∠ECF、∠HEC=∠ECF、∠IEC=∠ECF。HCに注目すると、まず同位角が∠AHI=∠HCF、∠AHE=∠HCF、錯角が∠DHC=∠HCF、∠GHC=∠HCF。GCに注目すると、錯角が∠DGC=∠GCF。DCに注目すると、無し。
しかしこうしてみると、様々な辺で角を共有して考える、というのはかなり便利な方法だと分かる。明らかにこの方法は効率的では無いので、何とか改良したい。
あと、交差している線で向かい合う角は、お互いにイコール、というのも定理なのだなと。辺が2つに分けられた場合、一方=180° - もう一方、というようなのも定理だし。平行線の定理というかチェックは、それとセットなんだなと分かった。休憩。
結局、DとFを固定して、∠DEC=∠ECFであれば、その間の点Gと点Hについてそれぞれ、∠GEC, ∠HEC = ∠ECF、という風に追加すれば良いのかもしれない。
今回は上の辺だけがいっぱいあるわけだが、本当は下の辺もいっぱいあるかもしれなくて、その場合は掛け算みたいに確認する数が増えてしまう。だから計算量的に、そっちの方が良いかもしれない。
いや、錯角っていうのは多分大きな角でも錯角なわけで、だとしたら短い辺により長い辺を付け加えていった方が良いのか?分からん。まあでも本質的にはどっちでも同じことなのかもしれんが。
確認する際も、平行と交わる時にできる4つの角について、1つずつ確認していった方が良いだろうな。
EFは無し。
ECが、上の平行線と成立しているのが右下の角で、下の平行線で成立しているのが左上の角で、∠IEC=∠ECFで、∠IECについてHとGとDが付く。
HCは、上の平行線では全ての角が成立していて、下の平行線では左上の角が成立していて、左上の同位角が∠AHI=∠HCFで、∠AHIについてEが付く。右下の錯角が∠GHC=∠HCFで、∠GHCについてDが付く。
GCは、上の平行線では左上と左下の角が成立していて、下の平行線では左上の角が成立していて、左下について確認した後に、右下の錯角が∠DGC=∠GCFで、両方に何も付かない。
DCは、上の平行線で左下の角が成立しているが、何も無し。
こんな感じで全部確認できたかな。
大きな平行線を見つけて、それを結ぶ辺を見つけて、その辺でできる上の4角と下の4角を確認して、上の4角を基準に順番に成立している錯角と同位角を追加していく、追加した際には辺を伸ばす形で辿っていってどんどん結びつけていく、と。
休憩するか。
結局ユークリッド幾何学は、角度の演算とでも言うべき何かなのであって、グラフで考えているからおかしくなるのかもしれない。
平行線を見つけて、それに跨る辺を見つけて、同位角と錯角で同じものを記していく、という所までが人間がやっている所なのであって、それ以降はやっていない。
では、三角形の内角の確認に移る。
ってよく見たら平行四辺形なのか。それなら対角線はそれぞれ縦横の平行線で錯角になるし、だからそれを合わせた向かい合う角も同じになる。仕切り直すか。