03年度ファイナル問題 問題2
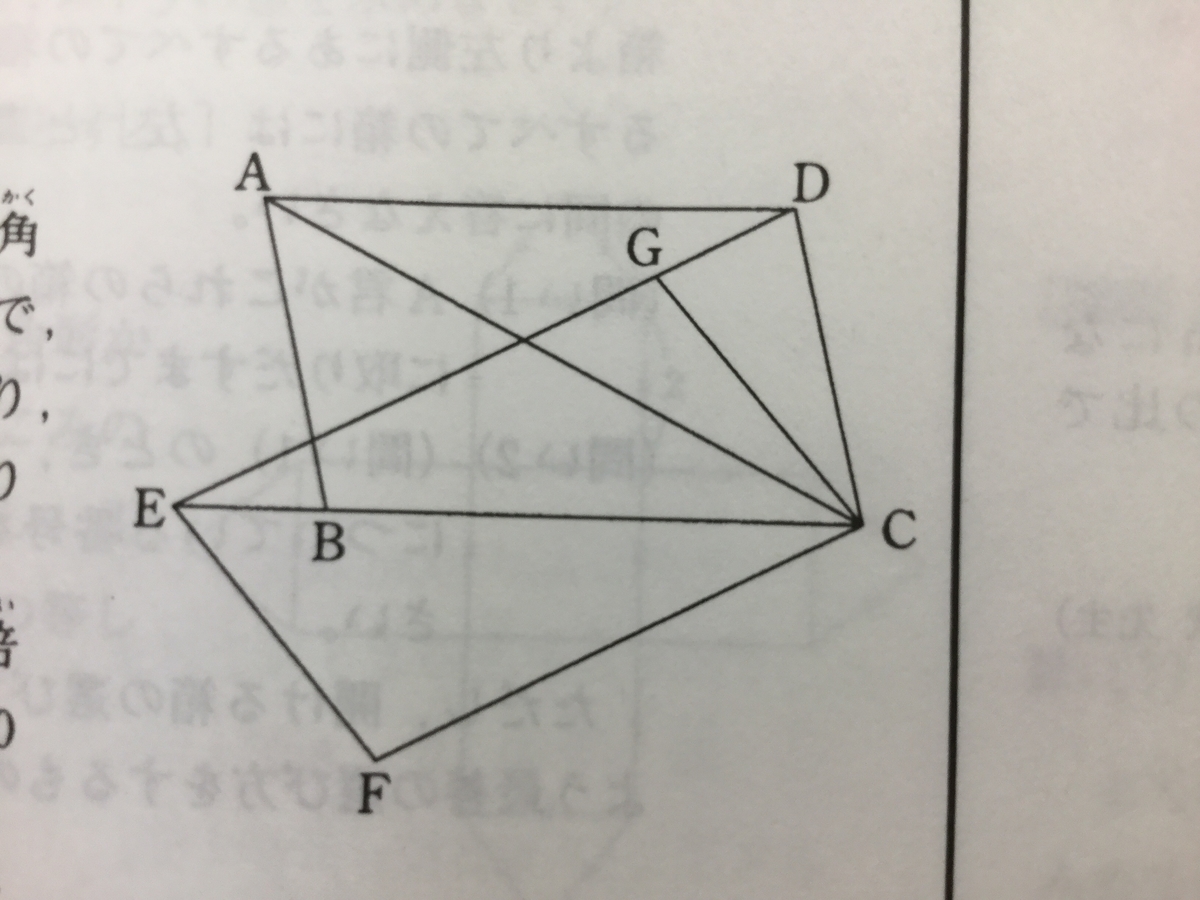
『右の図の四角形ABCDと四角形EFCGは合同な平行四辺形で、辺EGを延長した線は点Dを通り、辺CBを延長した線は点Eを通ります。
このとき、角BACの[ア]倍と角CADの[イ]倍の和は180度となります。
[ア]、[イ]に入る整数をそれぞれ答えなさい。
 』
』
またもややり直し。
まずは名付けられていない交点に上からH、Iと名付ける。
平行線と三角形と、対頂角が発生する交点を見つける。
平行線は、ADとEC、ABとDC、EDとFC、EFとGC。
対頂角が発生する交点は、点を一つずつ見ていって、H、I。
三角形は、これは昨日のを流用する。
ABC、ACD、ADH、ADI、AHI。
BEI。
CDE、CDG、CDH、CEF、CEG、CEH、CGH。
今回は先に、対頂角のイコールを繋げておく。
点Hでは、∠AHG=∠IHC、∠AHI=∠GHC。
点Iでは、∠AIH=∠EIB、∠AIE=∠HIB。
次に、平行線の同位角と錯角をイコールで繋いでいく。
平行線ADとECに跨る辺は、ADを辿っていって、AB、AC、DE、DC。
ABでは、上の平行線においては右下の角が成立していて、下の平行線においては左上と右上の角が成立している。右下の錯角が左上なので、∠DAI=∠IBE。
ACでは、上の平行線においては右下の角が成立していて、下の平行線においては左上の角が成立している。右下の錯角は左上なので、∠DAH=∠HCB。
DEでは、上の平行線においては左下の角が成立していて、下の平行線においては右上の角が成立している。左下の錯角は右上なので、∠ADG=∠IEB。
DCでは、上の平行線においては左下の角が成立していて、下の平行線においては左上の角が成立している。左下の同位角も錯角も無いので、無し。(休憩)
平行線ABとDCを跨る辺は、AD、AC、ID、BC。
ADでは、左の平行線においては右下の角が成立していて、右の平行線においては左下の角が成立している。右下の同位角も錯角も無いので、無し。
ACでは、左の平行線においては右下の角が成立していて、右の平行線においては左上の角が成立している。右下の錯角は左上なので、∠HAI=∠HCD。
IDでは、左の平行線においては全ての角が成立していて、右の平行線においては左下の角が成立している。右上の錯角は左下なので、∠AIH=∠GDC。左下の同位角は左下なので、∠EIB=∠GDC。
BCでは、左の平行線においては左上と右上の角が成立していて、右の平行線においては左上の角が成立している。左上の同位角は左上なので、∠IBE=∠DCB。
平行線EDとFCを跨る辺は、EC、HC、GC、DC。
ECでは、上の平行線においては右下の角が成立していて、下の平行線においては左上の角が成立している。右下の錯角は左上なので、∠IEB=∠BCF。
HCでは、上の平行線においては全ての角が成立していて、下の平行線においては左上の角が成立している。左上の同位角は左上なので、∠AHI=∠HCF。右下の錯角は左上なので、∠GHC=∠HCF。
GCでは、上の平行線においては左下と右下の角が成立していて、下の平行線においては左上の角が成立している。右下の錯角は左上なので、∠GDC=∠GCF。
DCでは、上の平行線においては左下の角が成立していて、下の平行線においては左上の角が成立している。左下の同位角も錯角も無いので、無し。
平行線EFとGCを跨る辺は、EG、EC、FC。
EGでは、左の平行線においては右下の角が成立していて、右の平行線においては左下と右下の角が成立している。右下の同位角は右下なので、∠IEF=∠DGC。
ECでは、左の平行線においては右下の角が成立していて、右の平行線においては左上の角が成立している。右下の錯角は左上なので、∠BEF=∠GCB。
FCでは、左の平行線においては右上の角が成立していて、右の平行線においては左上の角が成立している。右上の同位角も錯角も無いので、無し。
よって、
∠DAI=∠IBE。
∠DAH=∠HCB。
∠ADG=∠IEB。
∠HAI=∠HCD。
∠AIH=∠GDC。∠EIB=∠GDC。
∠IBE=∠DCB。
∠IEB=∠BCF。
∠AHI=∠HCF。∠GHC=∠HCF。
∠GDC=∠GCF。
∠IEF=∠DGC。
∠BEF=∠GCB。
休憩して、次は「X=Y、Y=X」となっているものを統合していく。
上から地道に確認していこう。先に対頂角から確認しようかな。
対頂角のイコールは、∠AHG=∠IHC、∠AHI=∠GHC。∠AIH=∠EIB、∠AIE=∠HIB。
∠AHGは無い。∠IHCは無い。
∠AHIはあった。∠AHI=∠HCF。よって、∠AHI=∠HCF=∠GHC。∠GHCもあったが、∠GHC=∠HCFで、同じ。
∠AIHはあった。∠AIH=∠GDC。よって、∠AIH=∠GDC=∠EIB。∠EIBもあったが、∠EIB=∠GDCで、同じ。
∠AIEは無い。∠HIBも無い。
イコールのリストを更新して、
∠DAI=∠IBE。
∠DAH=∠HCB。
∠ADG=∠IEB。
∠HAI=∠HCD。
∠AIH=∠GDC=∠EIB。
∠IBE=∠DCB。
∠IEB=∠BCF。
∠AHI=∠HCF=∠GHC。
∠GDC=∠GCF。
∠IEF=∠DGC。
∠BEF=∠GCB。
先に平行線のイコールを統合した方が良かったかな?じゃあ気を取り直して上から調べていく。
∠DAIは無い。∠IBEはあった。∠IBE=∠DCB。よって、∠DAI=∠IBE=∠DCB。
∠DAHは無い。∠HCBは無い。
∠ADGは無い。∠IEBはあった。∠IEB=∠BCF。よって、∠ADG=∠IEB=∠BCF。
∠HAIは無い。∠HCDは無い。
∠AIHは無い。∠GDCはあった。∠GDC=∠GCF。よって、∠AIH=∠GDC=∠EIB=∠GCF。∠EIBは無い。
∠IBEはもうやった。∠DCBは無い。
∠IEBはもうやった。∠BCFは無い。
∠AHIは無い。∠HCFは無い。∠GHCは無い。
∠GDCはもうやった。∠GCFは無い。
∠IEFは無い。∠DGCは無い。
∠BEFは無い。∠GCBは無い。
統合後は、
∠DAI=∠IBE=∠DCB。
∠DAH=∠HCB。
∠ADG=∠IEB=∠BCF。
∠HAI=∠HCD。
∠AIH=∠GDC=∠EIB=∠GCF。
∠AHI=∠HCF=∠GHC。
∠IEF=∠DGC。
∠BEF=∠GCB。
これらが対頂角と平行線の同位角と錯角のイコールを統合した後の表で、まあ文句無しかな。休憩後は三角形の内角を見ていく。
三角形を基準に見ていく。
ABC、ACD、ADH、ADI、AHI。
BEI。
CDE、CDG、CDH、CEF、CEG、CEH、CGH。
三角形ABCが持つ角は、∠HAI、∠IBC、∠HCB。
三角形ACDが持つ角は、∠DAH、∠HCD、∠ADC。
三角形ADHが持つ角は、∠DAH、∠GHA、∠ADG。
三角形ADIが持つ角は、∠ADH、∠HIA、∠DAI。
三角形AHIが持つ角は、∠HAI、∠AIH、∠IHA。
三角形BEIが持つ角は、∠BEI、∠DIB、∠IBD。
三角形CDEが持つ角は、∠GDC、∠DCB、∠IEB。
三角形CDGが持つ角は、∠CDG、∠DGC、∠GCD。
三角形CDHが持つ角は、∠DCH、∠CHG、∠GDC。
三角形CEFが持つ角は、∠BCF、∠CFE、∠FEB。
三角形CEGが持つ角は、∠GCB、∠BEI、∠HGC。
三角形CEHが持つ角は、∠HCB、∠BEI、∠IHC。
三角形CGHが持つ角は、∠CGH、∠GHC、∠HCG。
これはめんどくさいな。ちょっと休憩して考えてみるか。
えーっと、考えてみて、あの統合されたイコールに順番など無いが、仮に上から[0]、[1]、[2]という風に名付けていくとして、こうなる。
三角形ABCが持つ角は、[3], ∠IBC, [1]。
三角形ACDが持つ角は、[1], [3], ∠ADC。
三角形ADHが持つ角は、[1], ∠GHA, [2]。
三角形ADIが持つ角は、∠ADH, [4], [0]。
三角形AHIが持つ角は、[3], [4], [5]。
三角形BEIが持つ角は、[2], [4], [0]。
三角形CDEが持つ角は、[4], [0], [2]。
三角形CDGが持つ角は、[4], [6], ∠GCD。
三角形CDHが持つ角は、∠DCH, [5], [4]。
三角形CEFが持つ角は、[2], ∠CFE, [7]。
三角形CEGが持つ角は、[7], [2], ∠HGC。
三角形CEHが持つ角は、[1], [2], ∠IHC。
三角形CGHが持つ角は、∠CGH, [5], ∠HCG。
三角形の内角は180°だから、三角形の角の2つが同じ大きさであれば、残り1つも同じ大きさ。上から見ていく。
ABCは、2番目のACDと同じ。∠IBC=∠ADC。かつ、三角形ABCとACDは相似だ。
2番目は抜かすとして、ADHは、下から2番めのCEHと同じ。∠GHA=∠IHC。かつ、ADHとCEHは相似だ。
ADIは、BEI、CDEと同じ。∠ADH=[2]。かつ、ADIとBEIとCDEは相似。
AHIは、CDHと同じ。∠DCH=[3]。かつ、AHIとCDHは相似。
CDEは、何とも同じじゃない。
CDGは、何とも同じじゃない。
CEFは、CEGと同じ。∠CFE=∠HGC。かつCEFとCEGは相似。
CEHはもうやったので抜かすとして、CGHは1つだしそもそも最後なので調べる必要すら無い。
∠DAI=∠IBE=∠DCB。
∠DAH=∠HCB。
∠ADG=∠IEB=∠BCF=∠ADH。
∠HAI=∠HCD=∠DCH。
∠AIH=∠GDC=∠EIB=∠GCF。
∠AHI=∠HCF=∠GHC。
∠IEF=∠DGC。
∠BEF=∠GCB。
∠IBC=∠ADC。
∠GHA=∠IHC。
∠CFE=∠HGC。
三角形ABCとACDは相似。
ADHとCEHは相似。
ADIとBEIとCDEは相似。
AHIとCDHは相似。
CEFとCEGは相似。
ミスを発見してしまった。休憩後に直しておくので、気付かないだろう。休憩。
えーっと、次に、外角は他の内角2つと同じか。三角形を一つずつ確認していく。
ABC、ACD、ADH、ADI、AHI。
BEI。
CDE、CDG、CDH、CEF、CEG、CEH、CGH。
ABCの外角はBCを延長した先にある∠IBEで、∠HAI+∠HCB。[0] = [3] + [1]。
ACDは、どの辺も延長されてないので、外角は無し。
ADHは、AHを延長した先にある∠AHIと、DHを延長した先にある∠GHCで、∠DAH+∠ADG。[5] = [1] + [2]。
ADIは、DIを延長した先にある∠AIEと、AIを延長した先にある∠HIBで、∠DAI+∠ADG。
「∠AIE=∠HIB」を追加するのを忘れていたか。
まあ、とにかく、いや流石に今日はやりきろう。
[それらX] = [0] + [2]。
AHIは、∠AIE、∠AHG、∠IHC、∠HIBが外角。∠AIE, ∠HIB = ∠HAI + ∠AHI。[それらX] = [3] + [5]。
「∠IBC=∠ADC」は[8]としよう、以下も同じく[9]、[10]。
[9] = ∠HAI + ∠HIA。[9] = [3] + [4]。
BEIは、∠IBC、∠HIB、∠AIEが外角。∠IBC = ∠BEI + ∠BIE。[8] = [2] + [4]。
∠HIB, ∠AIE = ∠IEB + ∠IBE。[それらX] = [2] + [0]。
ちょっと休憩しよう。精神ダメージが大きい。
CDEは、外角は無し。
CDGは、∠CGHが外角。∠CGH = ∠GDC + ∠DCG。∠CGH = [4] + ∠DCG。
CDHは、∠GHAとその対頂角がそれぞれ外角で、[9] = ∠DCH + ∠GDC。[9] = [3] + [4]。
CEFは、外角無し。
CEGは、∠DGCが外角。∠DGC = ∠IEB + ∠GCB。[6] = [2] + [7]。
CEHは、∠AHIとその対頂角がそれぞれ外角で、[5] = ∠IEB + ∠HCB。[5] = [2] + [1]。
CGHは、∠DGCと、∠AHGとその対頂角が外角。∠DGC = ∠GHC + ∠GCH。[6] = [5] + ∠HCG。
これで全部か。
[0] = [3] + [1]。
[5] = [1] + [2]。
[それらX] = [0] + [2]。
[9] = [3] + [4]。
[それらX] = [2] + [0]。
∠CGH = [4] + ∠DCG。
[9] = [3] + [4]。
[6] = [2] + [7]。
[5] = [2] + [1]。
[6] = [5] + ∠HCG。
つまり、
[0] = [1] + [3]。
[5] = [1] + [2]。
[それらX] = [0] + [2]。
[9] = [3] + [4]。
[6] = [2] + [7]。
∠CGH = [4] + ∠DCG。
[6] = [5] + ∠GCH。(ちょっと中心以外をアルファベット順にした)
休憩。
次は二等辺三角形に移るわけだが、その前に問題を確認しておく。
∠IAHの?倍と∠HADの?倍の和は180°か。[3] * ? + [1] * ? = 180。
[0] = [1] + [3]。
[5] = [1] + [2]。
[9] = [3] + [4]。
えーっと、何と何を足せば180°なんだろう。外角を観察すると、とりあえず全部、三角形の内角に置き換え可能か。
三角形AHIが持つ角は、[3], [4], [5]。
三角形BEIが持つ角は、[2], [4], [0]。
三角形CDEが持つ角は、[4], [0], [2]。
三角形CDGが持つ角は、[4], [6], ∠DCG。
三角形CEGが持つ角は、[7], [2], ∠CGH。
三角形CGHが持つ角は、∠CGH, [5], ∠GCH。
今のところ、イコールとかじゃない角が出てくるとしたら、最後の以外の2つでバランスを取る感じか。
([4] + [6] + ∠DCG) + ([7] + [2] + ∠CGH) = 360°。いや全然分からんな。
残りのは[4]だから「[9] = [3] + [4]」が重要なのか?でも[9]か。はあ。
じゃあとりあえず二等辺三角形に移るか。休憩。
しかし、三角形の2角が等しいということも無いし、2辺分かっているということも無いし。
当初の予定では最初に戻ってループするつもりだったけど、平行線によるイコールの関係は書き出したし、内角も外角もやることはやった気がする。実はこの問題は作図が無い問題なのだけど。
[5] + [9] = 180°、[4] + [それらX] = 180°、というのもあったか。
いや分からんな。答えを見るか。休憩しよう。
答えを見ると、平行四辺形の同じ角を二等分しているので、[2] = [7]。同じものから同じものを引いているので、∠GCD = [1]。
CDとCGは同じ長さの辺なので、[4] = [6]。
えーっと、その次に∠CGD=∠ABE=∠BADというのが出てくるけど、分からない。
そこから、三角形CDGの内角の和を使って答えを求めるらしいが。
ちょっと書き方に問題があったので、もう一回ほど、同じ問題をやりたい。あと、いろいろ足りない部分があったから、それを何とかする必要もある。