03年度ファイナル問題 問題2
『右の図の四角形ABCDと四角形EFCGは合同な平行四辺形で、辺EGを延長した線は点Dを通り、辺CBを延長した線は点Eを通ります。
このとき、角BACの[ア]倍と角CADの[イ]倍の和は180度となります。
[ア]、[イ]に入る整数をそれぞれ答えなさい。
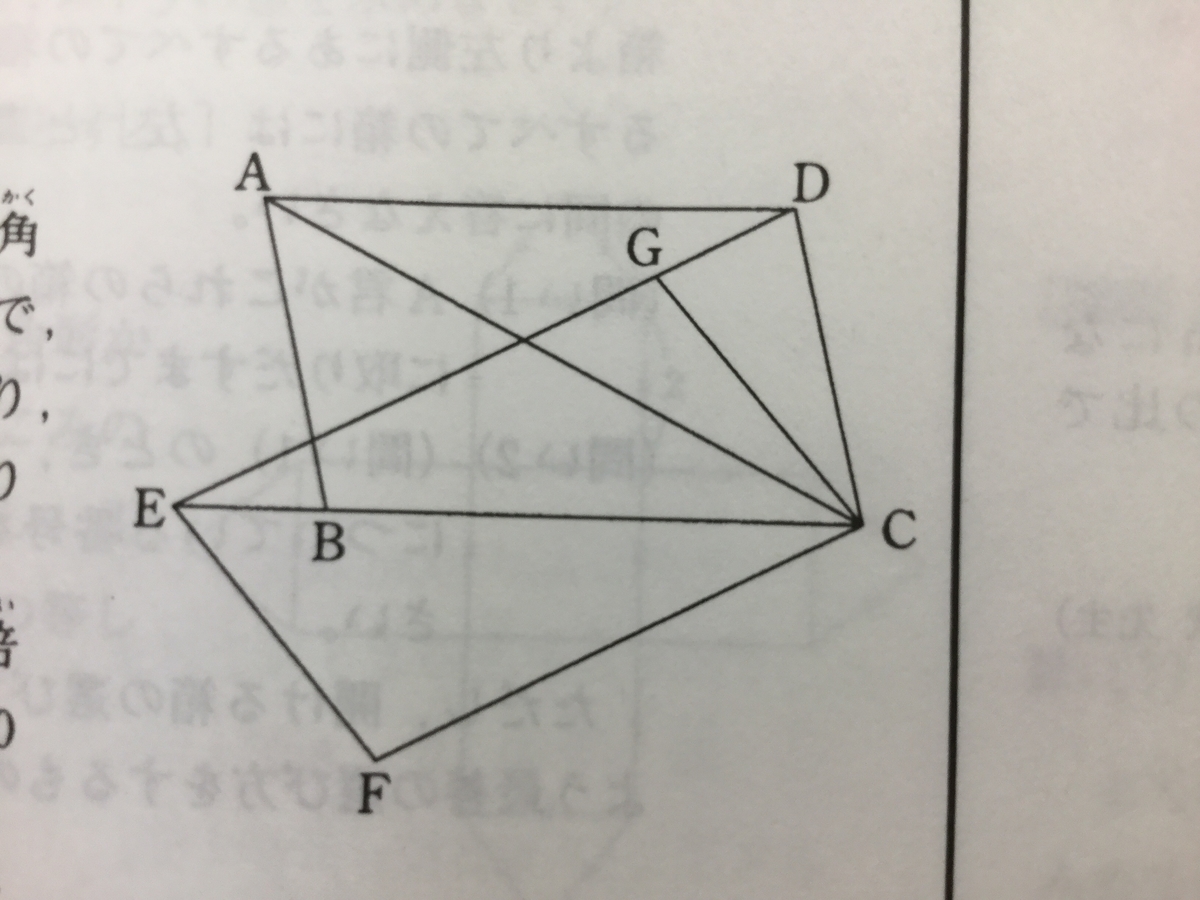 』
』
同じ問題を3回目。
まず名付けられていない交点を上からH、Iと名付ける。
三角形を探す。直線で繋がる点が他の直線で繋がる点と繋がっていたら三角形と見なす。ただし同一直線上は除く。
基準の点。直線で繋がる点。結果見つかった三角形。
A。B、C、D、H、I。ABC、ACD、ADH、ADI、AHI。
B。C、E、I。BEI。
C。D、E、F、G、H。CDE、CDG、CDH、CEF、CEG、CEH、CGH。
D。E、G、H、I。
E。F、G、H、I。
F。
G。H、I。
見つかった三角形。その三角形の角。
ABC。BCH、CBI、HAI。
ACD。ADC、DAH、DCH。
ADH。ADG、AHG、DAH。
ADI。ADG、AIH、DAH。
AHI。AHI、AIH、HAI。
BEI。BEI、BIE、EBI。
CDE。BCD、BEI、CDG。
CDG。CDG、CGD、DCG。
CDH。CDG、CHG、DCH。
CEF。BCF、BEF、CFE。
CEG。BCG、BEI、CGH。
CEH。BCH、BEI、CHI。
CGH。CGH、CHG、GCH。
問題文から、平行四辺形の同じ長さの辺と角を記述しておく。(しかし振り返れば先に三角形を探すべきだった)
同じ長さの辺。
AD、BC、EG、CF。
AB、CD、EF、CG。
同じ大きさの角。
DAI、FEI。
ADC、CGH。
CBI、CFE。
BCD、FCG。
対頂角が発生する点をアルファベット順に調べて見つけ、イコールの角を記述しておく。
同じ大きさの角。
AHG、CHI。
AHI、CHG。
AIH、BIE。
AIE、BIH。
平行線とそれに跨る辺を調べ、同位角と錯角を同じ大きさの角として記述していく。
平行線。跨る辺。 同じ大きさの角。
AD、EC。AB、AC、DE、DC。 EBI、DAI。DAH、BCH。ADG、BEI。
AB、DC。AD、AC、BC。 HAI、DCH。
ED、FC。EF、EC、HC、GC、DC。 BEI、BCF。AHI、CHG、FCH。CGD、FCG。
EF、GC。EG、EC、FC。 FEI、CGD。BEI、BCF。
合同の平行四辺形、対頂角、平行線の、同じ大きさの角を統合する。文章内検索で探す。番号を付けていく。
同じ大きさの角。
0 : BCD、CGD、DAI、EBI、FCG、FEI。
1 : ADC、CGH。
2 : CBI、CFE。
3 : AHG、CHI。
4 : AHI、CHG、FCH。
5 : AIH、BIE。
6 : AIE、BIH。
7 : BCH、DAH。
8 : ADG、BCF、BEI。
9 : DCH、HAI。
点を一つずつ見ていって、どの角を足したらどの角になるか確認していく。くどいようだが文章内検索を使う。
確認した点。角の足し算
A。[7] + [9] = [0]
B。[0] + [2] = 180°
C。[0] + DCG = DCF
C。[0] + [8] = DCF
C。[4] + [9] = DCF
C。BCG + [8] + DCG = DCF
C。[8] + [7] + GCH + DCG = DCF
C。[4] + GCH = [0]
C。BCG + [8] = [0]
C。BCG + DCG = [0]
C。[9] + [7] = [0]
C。[8] + [7] + GCH = [0]
C。[7] + GCH + DCG = [0]
C。[8] + [7] = [4]
C。[7] + GCH = BCG
C。GCH + DCG = [9]
D。[8] + CDG = [1]
E。[8] + BEF = [0]
G。[0] + [1] = 180°
H。[3] + [4] = 180°
H。[4] + [3] = 180°
H。[3] + [4] = 180°
H。[4] + [3] = 180°
I。[5] + [6] = 180°
I。[6] + [5] = 180°
ごちゃごちゃしていて難しいので、まだ使わない。
三角形の内角や外角を調べるために、角が何と同じかを一覧にしておく。文章内検索を使うと便利。
三角形。角。
ABC。[7]、[2]、[9]。
ACD。[1]、[7]、[9]。
ADH。[8]、[3]、[7]。
ADI。[8]、[5]、[7]。
AHI。[4]、[5]、[9]。
BEI。[8]、[5]、[0]。
CDE。[0]、[8]、CDG。
CDG。CDG、[0]、DCG。
CDH。CDG、[4]、[9]。
CEF。[8]、BEF、[2]。
CEG。BCG、[8]、[1]。
CEH。[7]、[8]、CHI。
CGH。[1]、[4]、GCH。
内角を調べる。2つが同じだったら、残りも同じ。上から調べていく。
三角形の組。結果。
ABC、ACD。[1] = [2]。
ADH、ADI。[3] = [5]。
ADH、CEH。CHI = [3]。(もうあったのに書いてしまった)
ADI、BEI。[7] = [0]。
AHI、CDH。CDG = [5]。
BEI、CDE。CDG = [5]。
更新された同じ大きさの角。
0 : BCD、CGD、DAI、EBI、FCG、FEI、BCH、DAH。
1 : ADC、CGH、CBI、CFE。
2 :
3 : AHG、CHI、AIH、BIE、CDG。
4 : AHI、CHG、FCH。
5 :
6 : AIE、BIH。
7 :
8 : ADG、BCF、BEI。
9 : DCH、HAI。
三角形。更新された角。
ABC。[0]、[1]、[9]。
ACD。[0]、[1]、[9]。
ADH。[0]、[3]、[8]。
ADI。[0]、[3]、[8]。
BEI。[0]、[3]、[8]。
CDE。[0]、[3]、[8]。
CEH。[0]、[3]、[8]。
AHI。[3]、[4]、[9]。
CDH。[3]、[4]、[9]。
CDG。[0]、[3]、DCG。
CGH。[1]、[4]、GCH。
CEF。[1]、[8]、BEF。
CEG。[1]、[8]、BCG。
いろいろ追加。
DCG = [8]。
BEF = BCG。
またまた更新された同じ大きさの角。
0 : BCD、CGD、DAI、EBI、FCG、FEI、BCH、DAH。
1 : ADC、CGH、CBI、CFE。
2 :
3 : AHG、CHI、AIH、BIE、CDG。
4 : AHI、CHG、FCH。
5 :
6 : AIE、BIH。
7 :
8 : ADG、BCF、BEI、DCG。
9 : DCH、HAI。
10 : BCG、BEF。
三角形。また更新された角。
ABC。[0]、[1]、[9]。
ACD。[0]、[1]、[9]。
ADH。[0]、[3]、[8]。
ADI。[0]、[3]、[8]。
BEI。[0]、[3]、[8]。
CDE。[0]、[3]、[8]。
CDG。[0]、[3]、[8]。
CEH。[0]、[3]、[8]。
AHI。[3]、[4]、[9]。
CDH。[3]、[4]、[9]。
CEF。[1]、[8]、[10]。
CEG。[1]、[8]、[10]。
CGH。[1]、[4]、GCH。
三角形を基準にして、外角が発生する三角形を探していく。三角形の更新された角?には、元々の角も書いておいた方が良さそうだ。
三角形。結果。
ABC。[0] + [0] = [0]
ADH。[0] + [8] = [4]
ADI。[0] + [8] = [6]
AHI。[4] + [9] = [6]
AHI。[3] + [9] = [3]
BEI。[0] + [8] = [6]
BEI。[3] + [8] = [1]
CDG。[3] + [8] = [1]
CDH。[3] + [9] = [3]
CEG。[8] + [10] = [0]
CEH。[0] + [8] = [4]
CGH。[1] + GCH = [3]
CGH。[4] + GCH = [0]
ありゃ?どうやらどこかで間違えたらしい。
仕方ないなあ。明日もう一回やるか。
始めたばかりなんで、何回でもやって安定させたい。明日はこういう風な手順でやる予定だ。
三角形を探して角を記録。
問題文の合同な角(と辺)
対頂角
同位角、錯角
それらを統合
三角形の角がどう対応するか、名前を残したまま一覧に
三角形の内角。変化点を羅列するだけにする、一覧は手元で手を加えるだけにして、最後に一気に載せる。
外角
二等辺三角形
合同条件
角の足し算