03年度ファイナル問題 問題2
『右の図の四角形ABCDと四角形EFCGは合同な平行四辺形で、辺EGを延長した線は点Dを通り、辺CBを延長した線は点Eを通ります。
このとき、角BACの[ア]倍と角CADの[イ]倍の和は180度となります。
[ア]、[イ]に入る整数をそれぞれ答えなさい。
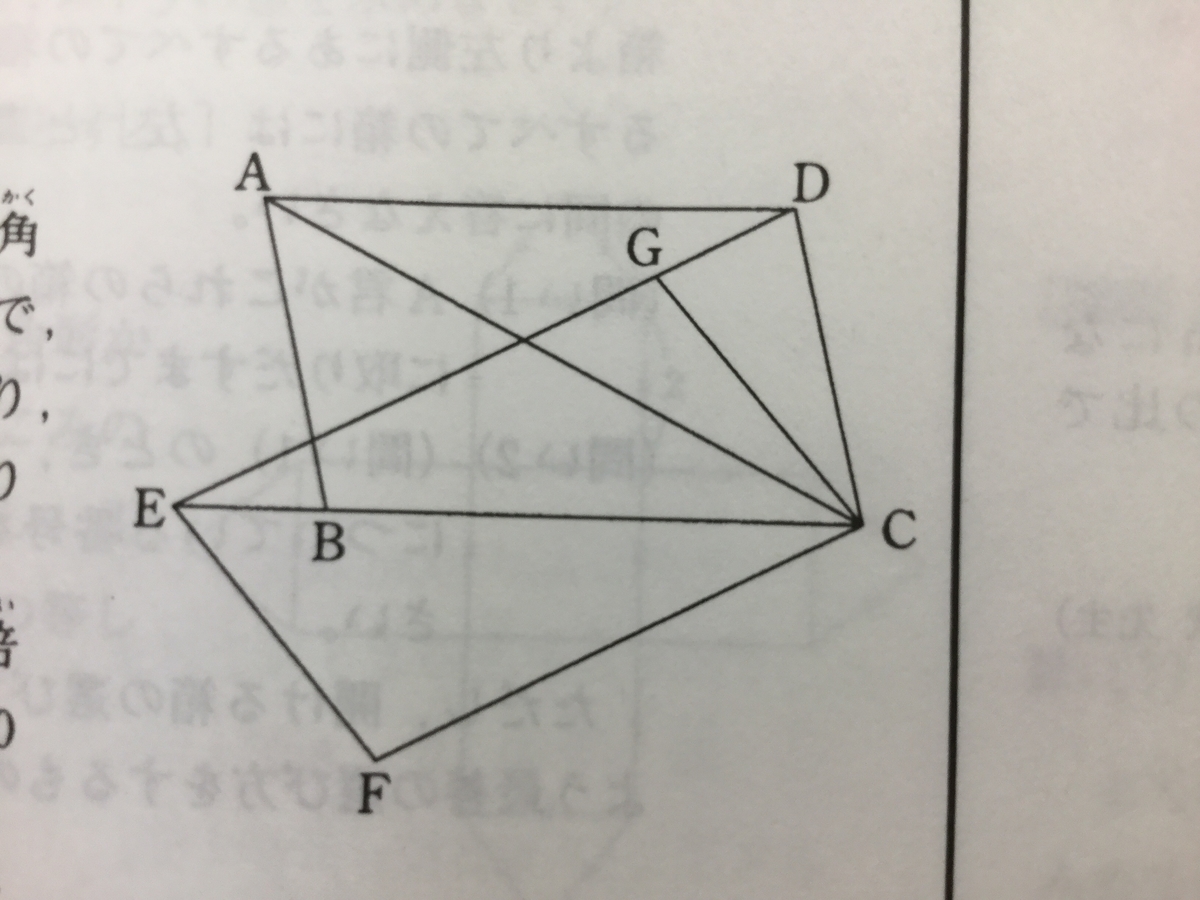 』
』
同じ問題を4回目となると、なかなかキツいものがある。今日で決めたいが。
まず名付けられていない交点をH、Iと名付ける。
三角形を見つけて、角を記録する。繋がっている点から更に別の繋がっている点に繋がっているなら、三角形。Aから。
探した点。繋がっている点。見つかった三角形。
A。B、C、D、H、I。ABC、ACD、ADH、ADI、AHI。
B。C、E、I。BEI。
C。D、E、F、G、H。CDE、CDG、CDH、CEF、CEG、CEH、CGH。
D。E、G、H、I。
E。F、G、H、I。
F。
G。H、I。
見つかった三角形。角。
ABC。HAI、CBI、BCH。
ACD。DAH、DCH、ADC。
ADH。DAH、ADG、AHG。
ADI。DAI、ADG、AIH。
AHI。HAI、AHI、AIH。
BEI。EBI、BEI、BIE。
CDE。BCD、CDG、BEI。
CDG。DCG、CDG、CGD。
CDH。DCH、CDG、CHG。
CEF。BCF、BEF、CFE。
CEG。BCG、BEI、CGH。
CEH。BCH、BEI、CHI。
CGH。GCH、CGH、CHG。
次に問題文から合同な辺や角を記録する。平行四辺形は、もう向き合う辺や角は等しいということを定義の一つと考えてしまう。
平行四辺形の等しい辺。
AD、BC、EG、CF。
AB、CD、EF、CG。
平行四辺形の等しい角。
DAI、BCD、FEI、FCG。
CBI、ADC、CFE、CGH。
対頂角の等しい角を記録する。点を基準に探していく。
探した点。対頂角の等しい角。
H。AHG、CHI。
H。AHI、CHG。
I。AIH、BIE。
I。AIE、BIH。
平行線の同位角と錯角を記録する。平行線に跨る辺は、平行線の一方を辿っていくことで見つける。
探した平行線。平行線に跨る辺。 見つかった同位角と錯角。
AD、CE。AB、AC、DE、CD。 DAI、EBI。DAH、BCH。ADG、BEI。
AB、CD。AD、AC、DI、BC。 HAI、DCH。AIH、CDG。EBI、BCD。
ED、FC。EF、CE、CH、CG、CD。 BEI、BCF。AHI、FCH。CHG、FCH。CGD、FCG。
EF、CG。EG、CE、CF。 FEI、CGD。BEF、BCG。
最後に問題文と対頂角と平行線の同位角と錯角を統合して、番号も付ける。文章内検索を使う。
0 : DAI、BCD、FEI、FCG、EBI、CGD。
1 : CBI、ADC、CFE、CGH。
2 : AHG、CHI。
3 : AHI、CHG、FCH。
4 : AIH、BIE、CDG。
5 : AIE、BIH。
6 : DAH、BCH
7 : ADG、BEI、BCF。
8 : HAI、DCH。
9 : BEF、BCG。
三角形の内角や外角を調べる際の下準備として、三角形の角とイコールの番号を紐付ける。文章内検索を使う。
ABC。HAI[8]、CBI[1]、BCH[6]。
ACD。DAH[6]、DCH[8]、ADC[1]。
ADH。DAH[6]、ADG[7]、AHG[2]。
ADI。DAI[0]、ADG[7]、AIH[4]。
AHI。HAI[8]、AHI[3]、AIH[4]。
BEI。EBI[0]、BEI[7]、BIE[4]。
CDE。BCD[0]、CDG[4]、BEI[7]。
CDG。DCG、CDG[4]、CGD[0]。
CDH。DCH[8]、CDG[4]、CHG[3]。
CEF。BCF[7]、BEF[9]、CFE[1]。
CEG。BCG[9]、BEI[7]、CGH[1]。
CEH。BCH[6]、BEI[7]、CHI[2]。
CGH。GCH、CGH[1]、CHG[3]。
内角を調べていく。一番上から、[1][6]の組み合わせは無いか、[1][8]は、[6][8]は、と調べていく。表は手元で更新していく。
三角形の組。結果。
ADI、CDG。DCG=[7]。
うん?昨日と随分結果が違うな。
ABC。HAI[8]、CBI[1]、BCH[6]。
ACD。DAH[6]、DCH[8]、ADC[1]。
ADH。DAH[6]、ADG[7]、AHG[2]。
ADI。DAI[0]、ADG[7]、AIH[4]。
AHI。HAI[8]、AHI[3]、AIH[4]。
BEI。EBI[0]、BEI[7]、BIE[4]。
CDE。BCD[0]、CDG[4]、BEI[7]。
CDG。DCG[7]、CDG[4]、CGD[0]。
CDH。DCH[8]、CDG[4]、CHG[3]。
CEF。BCF[7]、BEF[9]、CFE[1]。
CEG。BCG[9]、BEI[7]、CGH[1]。
CEH。BCH[6]、BEI[7]、CHI[2]。
CGH。GCH、CGH[1]、CHG[3]。
ちなみに、全部でこの6種類みたいだ。
[0][4][7]
[1][6][8]
[1][7][9]
[2][6][7]
[3][4][8]
[1][3][GCH]
次に外角を調べる。三角形を基準に見ていく。部分的に文章検索を使うと思考停止できて楽かも。
調べた三角形。結果。
ABC。[8] + [6] = [0]
ADH。[6] + [7] = [3]
ADI。[0] + [7] = [5]
AHI。[8] + [3] = [5]
AHI。[8] + [4] = [2]
BEI。[0] + [7] = [5]
BEI。[7] + [4] = [1]
CDG。[7] + [4] = [1]
CDH。[8] + [4] = [2]
CEG。[9] + [7] = [0]
CEH。[6] + [7] = [3]
CGH。GCH + [1] = [2]
CGH。GCH + [3] = [0]
ちなみに、これが結果一覧。
[8] + [6] = [0]
[9] + [7] = [0]
[7] + [4] = [1]
[8] + [4] = [2]
[6] + [7] = [3]
[0] + [7] = [5]
[8] + [3] = [5]
GCH + [3] = [0]
GCH + [1] = [2]
二等辺三角形の段階に入る。
二辺が同じ長さの三角形を調べる。これは簡単で、「AD、BC、EG、CF」、「AB、CD、EF、CG」のどちらかで、二回出てくるアルファベットを発見すれば良い。例えばBCとCFで、BとFが結ばれていたら、それは二等辺三角形。実際にはCDとCGが、DとGが辺で結ばれていて、二等辺三角形。
CGD = CDG、つまり[0] = [4]。手元で[4]を[0]に書き換えていく。
ABC。HAI[8]、CBI[1]、BCH[6]。
ACD。DAH[6]、DCH[8]、ADC[1]。
ADH。DAH[6]、ADG[7]、AHG[2]。
ADI。DAI[0]、ADG[7]、AIH[0]。
AHI。HAI[8]、AHI[3]、AIH[0]。
BEI。EBI[0]、BEI[7]、BIE[0]。
CDE。BCD[0]、CDG[0]、BEI[7]。
CDG。DCG[7]、CDG[0]、CGD[0]。
CDH。DCH[8]、CDG[0]、CHG[3]。
CEF。BCF[7]、BEF[9]、CFE[1]。
CEG。BCG[9]、BEI[7]、CGH[1]。
CEH。BCH[6]、BEI[7]、CHI[2]。
CGH。GCH、CGH[1]、CHG[3]。
次に、2角が同じ大きさの三角形を調べる。
すると、ADI、BEI、CDE、CDG、の4つが二等辺三角形だと分かる。
例えばADIだとDだけが角度が違うので、ADとDIがイコールだと分かる。
AD = DI。
BE = EI。
CE = DE。
CD = CG。
上の二等辺三角形の同じ長さの辺と統合するとこうなる。
同じ長さの辺。
AD、BC、EG、CF、DI。
AB、CD、EF、CG。
BE、EI。
CE、DE。
次に合同条件に入る。とりあえず、三角形を基準に見ていく。
一辺とそれを挟む角が同じかを見ていく。しかし、二角が同じということは、残りの一角も同じということで、そういうものだけ見ていけば良い。
並び替えてみる。
ADI。DAI[0]、ADG[7]、AIH[0]。
BEI。EBI[0]、BEI[7]、BIE[0]。
CDE。BCD[0]、CDG[0]、BEI[7]。
CDG。DCG[7]、CDG[0]、CGD[0]。
ABC。HAI[8]、CBI[1]、BCH[6]。
ACD。DAH[6]、DCH[8]、ADC[1]。
CEF。BCF[7]、BEF[9]、CFE[1]。
CEG。BCG[9]、BEI[7]、CGH[1]。
ADH。DAH[6]、ADG[7]、AHG[2]。
CEH。BCH[6]、BEI[7]、CHI[2]。
AHI。HAI[8]、AHI[3]、AIH[0]。
CDH。DCH[8]、CDG[0]、CHG[3]。
CGH。GCH、CGH[1]、CHG[3]。
合同な三角形。同じ長さの辺。
CDE、CDG。CDを共有。 っと思ったが、相似している辺に対応していないと合同では無いらしい。これは無し。
ABC、ACD。ACを共有。
CEF、CEG。CEを共有。
この2つは平行四辺形のやつなんで、特に成果無し。
次に、一角とそれを挟む二辺を見ていく。何を基準にやっていくのが最適なのか分からんが。とりあえず三角形で、二辺が同じなものを探そうか。
じゃあ急遽、辺にも番号を付けて。
同じ長さの辺。
0 : AD、BC、EG、CF、DI。
1 : AB、CD、EF、CG。
2 : BE、EI。
3 : CE、DE。
ABC。[1] [0] AC
ACD。AC [1] [0]
ADH。[0] DH AH
ADI。[0] [0] AI
AHI。AH HI AI
BEI。[2] [2] BI
CDE。[1] [3] [3]
CDG。[1] DG [1]
CDH。[1] DH CH
CEF。[3] [1] [0]
CEG。[3] [0] [1]
CEH。[3] EH CH
CGH。[1] GH CH
一番上から見ていくと、ユニークなACで共通するABCとACDはそもそも合同。次にside[0]とside[1]で共通するものを見ていくと、CEFとCEG。これも角を確かめるまでも無く、平行四辺形のもう一方なので合同だった。
ADHも、ユニークなDHから見ていく。CDHにDHがあったが、他で共通しない。次にAH。これも無い。
ADIも、[0]と[0]や、[0]とAIで共通するものは無し。
AHIも、二つ以上共通するものは無し。
BEIも、BIは共通しないし、[2] [2]も共通しない。
CDEは、[3] [3]か、[1] [3]なんだが、後者がCEFとCEGに該当。∠CDE = ∠CDG = angle[4]、∠CEF = ∠BEF = angle[9]なので、これも無し。
CDGも、DGも[1] [1]も無し。
CDHは、CHと[1]がCGHと該当。DCH = angle[7]、GCHがイコールに無い。のでとりあえず同じ角じゃない。
CEFとCEGは元々合同で、他の2つも特に無し。
やはり、成果は無かった。
手続き上、面積比と底辺比の法則もやらなきゃだけど、関係無いみたいだし、角の足し算を一覧で出す。点を基準にする。
A。DAH[6] + HAI[8] = DAI[0]
B。EBI[0] + CBI[1] = 180°
C。FCG[0] + DCG[7] = DCF
C。BCD[0] + BCF[7] = DCF
C。FCH[3] + DCH[8] = DCF
C。BCG[9] + BCF[7] + DCG[7] = DCF
C。FCH[3] + GCH = FCG[0]
C。BCG[9] + BCF[7] = FCG[0]
C。BCG[9] + DCG[7] = BCD[0]
C。DCH[8] + BCH[6] = BCD[0]
C。BCF[7] + BCH[6] = FCH[3]
C。BCH[6] + GCH = BCG[9]
C。GCH + DCG[7] = DCH[8]
D。ADG[7] + CDG[0] = ADC[1]
E。BEI[7] + BEF[9] = FEI[0]
G。CGD[0] + CGH[1] = 180°
H。AHG[2] + CHG[3] = 180°
I。AIH[0] + AIE[5] = 180°
GCHとDCFは不明なので、全部入れ終わったのかなと思う。
結果はこんな感じだ。
[6] + [8] = [0]
[7] + [9] = [0]
[0] + [7] = [1]
[6] + [7] = [3]
[0] + [1] = 180°
[2] + [3] = 180°
[0] + [5] = 180°
[0] + [7] = DCF
[3] + [8] = DCF
[7] + [7] + [9] = DCF
[3] + GCH = [0]
[7] + GCH = [8]
[6] + GCH = [9]
本当は一つでも明らかになったら、三角形の内角の和から繰り返さなきゃいけないのかな。これで答えが出れば良いけど。
問題文を読むと、角BAC = HAI = [8] が?倍と、角CAD = DAH = [6] が?倍の和は180°。
角の和と、外角のを統合すると、こうなる。
[0] + [1] = 180°
[0] + [5] = 180°
[2] + [3] = 180°
[6] + [8] = [0]
[7] + [9] = [0]
[0] + [7] = [1]
[0] + [8] = [2]
[6] + [7] = [3]
[0] + [7] = [5]
[3] + [8] = [5]
[0] + [7] = DCF
[3] + [8] = DCF
[7] + [7] + [9] = DCF
[3] + GCH = [0]
[1] + GCH = [2]
[7] + GCH = [8]
[6] + GCH = [9]
二つの値が同じなものの、残りはイコール。
元々の式 結果
[0] + [1] = 180°、[0] + [5] = 180° [1] = [5]
[0] + [7] = [1]、[0] + [7] = DCF DCF = [1]
こうなったわけだが、どうしたもんかな。
[0] + [1] = 180°
[2] + [3] = 180°
[6] + [8] = [0]
[0] + [8] = [2]
[7] + [9] = [0]
[0] + [7] = [1]
[3] + [8] = [1]
[6] + [7] = [3]
[3] + GCH = [0]
[1] + GCH = [2]
[7] + GCH = [8]
[6] + GCH = [9]
1 3 7 9
確か解答では、三角形の内角から180°を調達したんだっけか。この表と、三角形の角の表で、何とかなるのか。
[0][0][7] 7
[0][3][8] 3
[1][6][8] 1
[1][7][9]
[2][6][7] 7
[1][3][GCH]
もう答え見るか。
∠DCH = ∠BCG、つまり[8] = [9]、というのが欠けていた。
それが分かれば、例えば[7] + GCH = [8]、[6] + GCH = [9]から、[6] = [7]。答えに至っていた。
しかし、なぜ∠DCH = ∠BCG、というのが弾き出せなかったのか。課題だ。