03年度ファイナル問題 問題2
『右の図の四角形ABCDと四角形EFCGは合同な平行四辺形で、辺EGを延長した線は点Dを通り、辺CBを延長した線は点Eを通ります。
このとき、角BACの[ア]倍と角CADの[イ]倍の和は180度となります。
[ア]、[イ]に入る整数をそれぞれ答えなさい。
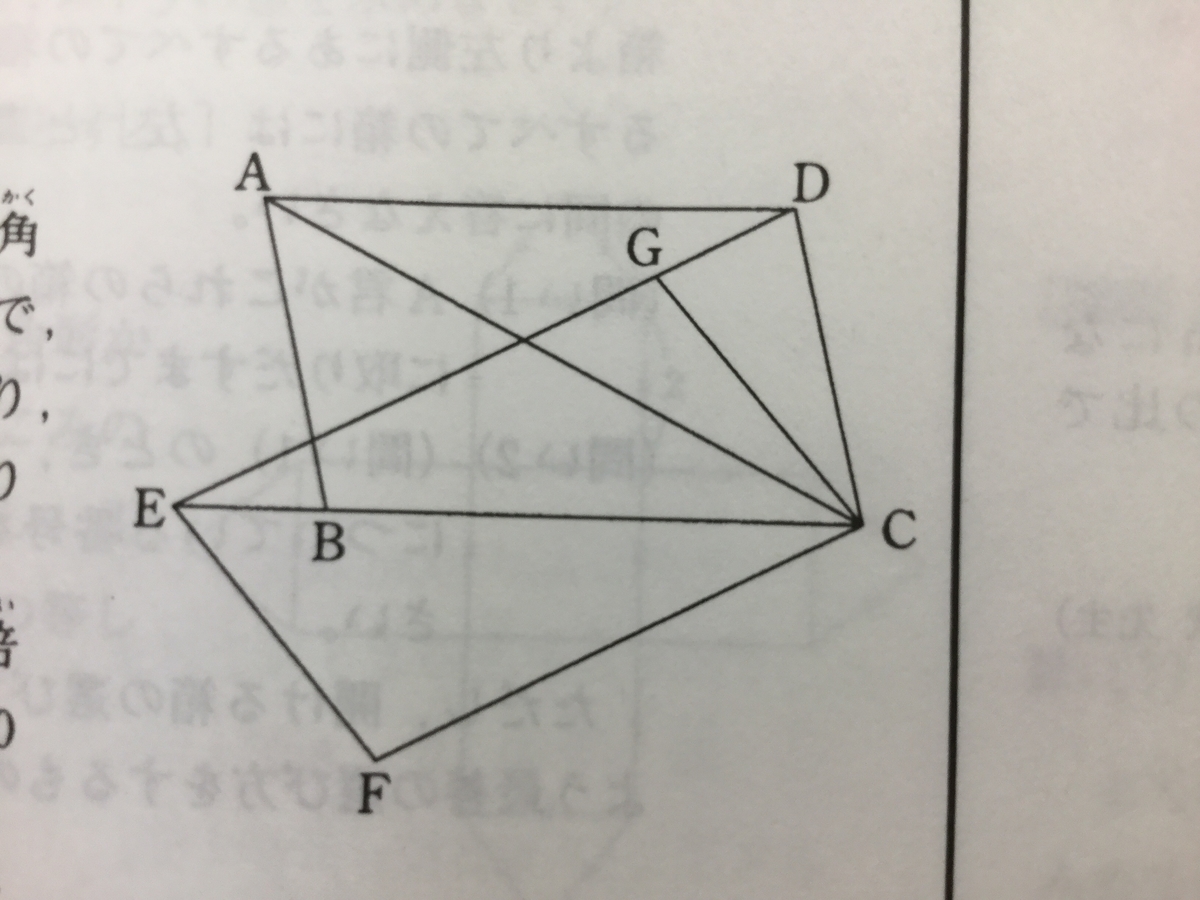 』
』
前回に同じ問題を4回目とか言っていたが、実際には5回目で、だから今回は同じ問題を6回目だ。今回で決めるつもりでいる。
名付けの段階
名前を付けていく。
無名の交点に、上からH、Iと名付けていく。
三角形を探していく。点に着目して、繋がっている点が更に繋がっている点と繋がっていたら、三角形。一直線上のものは抜かす。
着目した点。繋がっている点。 発見した三角形。
A。B、C、D、H、I。 ABC、ACD、ADH、ADI、AHI。
B。C、E、I。 BEI。
C。D、E、F、G、H。 CDE、CDG、CDH、CEF、CEG、CEH、CGH。
D。E、G、H、I。
E。F、G、H、I。
F。
G。H、I。
発見した三角形とその角と辺を記述する。
triangle := [
ABC : [HAI, AB, CBI, BC, BCH, AC],
ACD : [DAH, AC, DCH, CD, ADC, AD],
ADH : [DAH, AD, ADG, DH, AHG, AH],
ADI : [DAI, AD, ADG, DI, AIH, AI],
AHI : [HAI, AH, AHI, HI, AIH, AI],
BEI : [EBI, BE, BEI, EI, BIE, BI],
CDE : [BCD, CD, CDG, DE, BEI, CE],
CDG : [DCG, CD, CDG, DG, CGD, CG],
CDH : [DCH, CD, CDG, DH, CHG, CH],
CEF : [BCF, CE, BEF, EF, CFE, CF],
CEG : [BCG, CE, BEI, EG, CGH, CG],
CEH : [BCH, CE, BEI, EH, CHI, CH],
CGH : [GCH, CG, CGH, GH, CHG, CH]
]
設定の段階
問題文から設定を取得する。
平行四辺形は、向き合う辺や角は等しいというのを最初から定義として考えてしまう。
平行四辺形の等しい辺。
AD、BC、EG、CF。
AB、CD、EF、CG。
平行四辺形の等しい角。
DAI、BCD、FEI、FCG。
ADC、CBI、CFE、CGH。
対頂角の等しい角を記録する。点を基準に探していく。
探した点。 対頂角の等しい角。
H。 AHG、CHI。
H。 AHI、CHG。
I。 AIH、BIE。
I。 AIE、BIH。
平行線の同位角と錯角を記録していく。平行線を跨る辺は、平行線の一方を辿っていくことで見つける。
平行線の組。跨る辺。 同位角と錯角。
AD、CE。AB、AC、DE、CD。 DAI、EBI。DAH、BCH。ADG、BEI。
AB、CD。AD、AC、DI、BC。 HAI、DCH。BIE、CDG。AIH、CDG。EBI、BCD。
ED、CF。EF、CE、CH、CG、CD。 BEI、BCF。AHI、FCH。CHG、FCH。CGD、FCG。
EF、CG。EG、CE、CF。 FEI、CGD。BEI、BCF。
(しかし対頂角で同じなのは一つにまとめるべきだったかもしれない。BIE、AIH、CDG。というような感じで)
最後に定義と対頂角と同位角と錯角を統合する。文章内検索を使う。
side := [
[AD, BC, CF, EG],
[AB, CD, CG, EF]
]
angle := [
[DAI, BCD, FEI, FCG, EBI, CGD],
[CBI, ADC, CFE, CGH],
[AHG, CHI],
[AHI, CHG, FCH],
[AIH, BIE, CDG],
[AIE, BIH],
[DAH, BCH],
[ADG, BEI, BCF],
[HAI, DCH],
[BEF, BCG]
]
(実はangleはミスしたのに気付いて昨日のを流用している)
一つの三角形の段階
まず、三角形の辺や角と、辺や角のイコールを結びつける。文章内検索を使う。
triangle := [
ABC : [HAI[8], AB[1], CBI[1], BC[0], BCH[6], AC],
ACD : [DAH[6], AC, DCH[8], CD[1], ADC[1], AD[0]],
ADH : [DAH[6], AD[0], ADG[7], DH, AHG[2], AH],
ADI : [DAI[0], AD[0], ADG[7], DI, AIH[4], AI],
AHI : [HAI[8], AH, AHI[3], HI, AIH[4], AI],
BEI : [EBI[0], BE, BEI[7], EI, BIE[4], BI],
CDE : [BCD[0], CD[1], CDG[4], DE, BEI[7], EC],
CDG : [DCG, CD[1], CDG[4], DG, CGD[0], CG[1]],
CDH : [DCH[8], CD[1], CDG[4], DH, CHG[3], CH],
CEF : [BCF[7], CE, BEF[9], EF[1], CFE[1], CF[0]],
CEG : [BCG[9], CE, BEI[7], EG[0], CGH[1], CG[1]],
CEH : [BCH[6], CE, BEI[7], EH, CHI[2], CH],
CGH : [GCH, CG[1], CGH[1], GH, CHG[3], CH]
]
次に目視で、二角が同じな三角形を探す。上から、1と6、1と8、6と8、という具合で。もう探した数字の対は手元に控えておくと良いかもしれない。二角が同じであれば、残りの一角も同じ。
三角形の対。 結果。
ADI、CDG。 DCG = [7]。
同じ大きさの辺を2つ持つ三角形は二等辺三角形で、その2辺で共有する角以外の角はイコール。手元で表を更新していく。angleも(sideも)。
見つかった二等辺三角形。 結果。
CDG。 CDG[4] = CGD[0]。
(ここで更新した[0]だけに着目して、一つ上の内角をやり直しても良いかもしれない。そうした。)
同じ大きさの角を2つ持つ三角形は二等辺三角形で、その2角で共有する辺以外の辺はイコール。
見つかった二等辺三角形。 結果。
ADI。 AD[0] = DI。
CDG。 しかし一つ上の例。
(他のDIを探した。その後に、更新した[0]だけに着目して、一つ上の二等辺三角形をやり直した。)
二つの三角形の段階
次に、二つの三角形の関係を見ていく。合同条件。
まず、3辺の大きさが同じな三角形は合同から。何度もやり直すことになるので、制約が大きいものから取り掛かっていく。
しかし、そもそも3辺が明らかになっている三角形がまだ無かった。
次に、3角の大きさが同じで、更に対応する1辺の長さも同じな三角形を探す。
三角形の組。 結果。
ABC、ACD。 しかし辺は既に同じ。
ADH、CEH。 CE = [0]。
ADI、BEI。 BE = [0]。EI = [0]。
ADI、CDE。 DE = [0]。CD[1] = AI。
一つでも明らかになったので、この同じ3角と1辺の条件をもう一回やる。
三角形の組。 結果。
ADI、BEI。 BI = AI[1]。
AHI、CDH。 しかし辺は既に同じ。
CEF、CEG。 辺は既に同じ。
ちょっとミスっているな。まあ問題無かった。一つでも明らかになったのでもう一回やる。
「辺は既に同じ」なものも書いていたら膨大になるから、書かないことにしよう。変化無し。
同じ処理をくり返すことに必然性など無いのだけど、例えば[0][0][7]の3つの角と1辺で明らかになったものは、同じ条件で他のも明らかになりやすいというか、単に経験則的にそちらの方が良いというだけだと思うけど。まあなんか説明が下手だな。
一つでも明らかになって、同じ処理をくり返して新しいのが出なくなったら、一つ前の段階の「一つの三角形の段階」に戻って、その後更にこの段階を最初からやり直そうと思う。まあ人間もそうしていると思うんで。
(1回目のやり直し)
内角を確認したが、変化は無し。
二等辺三角形の辺のチェック。
三角形。 結果。
CEF。 BEF[9] = CFE[1]。
二等辺三角形の角のチェック。変化は無し。
一つの三角形の段階で変化があったので、もう一回段階をくり返す。
内角のチェックは変化は無し。
二等辺三角形の辺のチェックも変化は無し。
二等辺三角形の角のチェックも変化は無し。
では二つの三角形の段階に。
3辺が同じな三角形を探す。変化は無し。
3角と対応する1辺が同じな三角形を探す。変化は無し。
2辺とその間の角が同じな三角形を探す。
三角形の対。 結果。
ABC、CEF。 BEF[1] = HAI[8]。BCF[7] = BCH[6]。CE[0] = AC。
じゃあ同じ条件をもう1回。
三角形の対。 結果。
ABC、ADI。 DAI[0] = CBI[1]。
ってあれ?正三角形ができちゃったんだけど。流石にもう、やりたくないなあ。まあ、良いか。明日は旅行に行ってくるんで、その次の日にでも。