03年度ファイナル問題 問題2
『右の図の四角形ABCDと四角形EFCGは合同な平行四辺形で、辺EGを延長した線は点Dを通り、辺CBを延長した線は点Eを通ります。
このとき、角BACの[ア]倍と角CADの[イ]倍の和は180度となります。
[ア]、[イ]に入る整数をそれぞれ答えなさい。
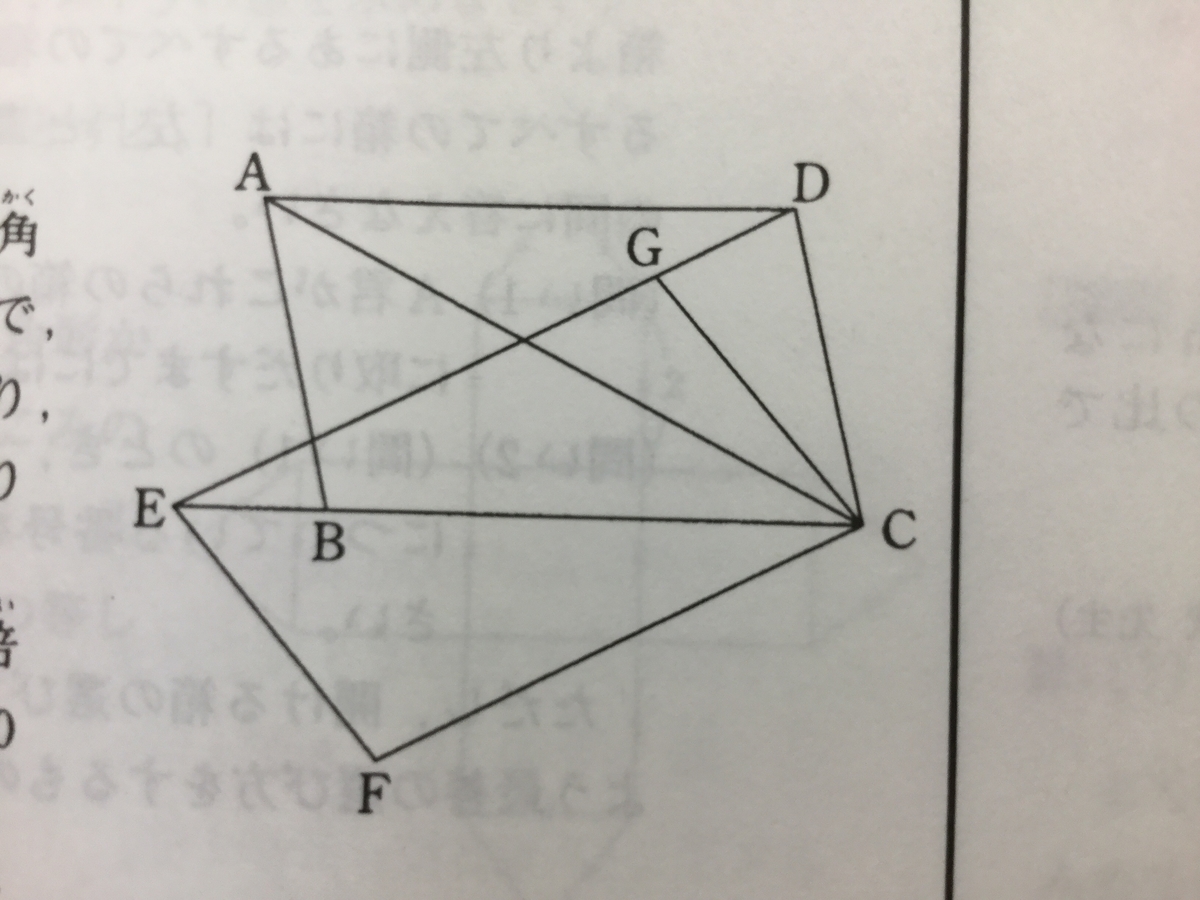 』
』
同じ問題を7回目。今日で決めるぞ!
セットアップ
まず、無名の交点に、上からH、Iと名付ける。
三角形を探す。点に着目して、繋がっている点から更に別の繋がっている点に繋がっていれば、それは三角形だ。
着目した点。繋がっている点。 発見した三角形。
A。B、C、D、H、I。 ABC、ACD、ADH、ADI、AHI。
B。C、E、I。 BEI。
C。D、E、F、G、H。 CDE、CDG、CDH、CEF、CEG、CEH、CGH。
D。E、G、H、I。
E。F、G、H、I。
F。
G。H、I。
発見した三角形をその角や辺と共に記述する。
triangle := [ #はてなの仕様で、行頭のスペースは反映されないみたいだ
ABC : [HAI, AB, CBI, BC, BCH, AC],
ACD : [DAH, AC, DCH, CD, ADC, AD],
ADH : [DAH, AD, ADG, DH, AHG, AH],
ADI : [DAI, AD, ADG, DI, AIH, AI],
AHI : [HAI, AH, AHI, HI, AIH, AI],
BEI : [EBI, BE, BEI, EI, BIE, BI],
CDE : [BCD, CD, CDG, DE, BEI, CE],
CDG : [DCG, CD, CDG, DG, CGD, CG],
CDH : [DCH, CD, CDG, DH, CHG, CH],
CEF : [BCF, CE, BEF, EF, CFE, CF],
CEG : [BCG, CE, BEI, EG, CGH, CG],
CEH : [BCH, CE, BEI, EH, CHI, CH],
CGH : [GCH, CG, CGH, GH, CHG, CH],
]
問題文から設定を取得する。平行四辺形は、向き合う辺や角は等しいというのを最初から定義として考えてしまう。
平行四辺形の等しい辺
AD、BC、EG、CF。
AB、CD、EF、CG。
平行四辺形の等しい角
DAI、BCD、FEI、FCG。
ADC、CBI、CFE、CGH。
対頂角の等しい角を記録する。点を基準に探していく。
見つけた対頂角。 等しい角。
H。 AHG、CHI。
H。 AHI、CHG。
I。 AIH、BIE。
I。 AIE、BIH。
平行線の同位角と錯角を記録する。平行線を跨る辺は、平行線の一方を辿ることで見つける。
平行線の組。跨る辺。 同位角と錯角。
AD、CE。AB、AC、DE、CD。 DAI、EBI。DAH、BCH。ADG、BEI。
AB、CD。AD、AC、DI、BC。 HAI、DCH。BIE、AIH、CDG。EBI、BCD。
DE、CF。CD、CG、CH、CE、EF。 CGD、FCG。AHI、CHG、FCH。BEI、BCF。
EF、CG。EG、CE、CF。 FEI、CGD。BEF、BCG。
等しい辺と等しい角をそれぞれ統合する。文章内検索を使う。
side := [
0 : [AD, BC, EG, CF],
1 : [AB, CD, EF, CG]
]
angle := [
0 : [DAI, BCD, FEI, FCG, EBI, CGD],
1 : [ADC, CBI, CFE, CGH],
2 : [AHG, CHI],
3 : [AHI, CHG, FCH],
4 : [AIH, BIE, CDG],
5 : [AIE, BIH],
6 : [DAH, BCH],
7 : [ADG, BEI, BCF],
8 : [HAI, DCH],
9 : [BEF, BCG]
]
最後に、三角形の辺や角と、これらの辺や角のイコールを結びつける。文章内検索を使う。
triangle := [
ABC : [HAI[8], AB[1], CBI[1], BC[0], BCH[6], AC],
ACD : [DAH[6], AC, DCH[8], CD[1], ADC[1], AD[0]],
ADH : [DAH[6], AD[0], ADG[7], DH, AHG[2], AH],
ADI : [DAI[0], AD[0], ADG[7], DI, AIH[4], AI],
AHI : [HAI[8], AH, AHI[3], HI, AIH[4], AI],
BEI : [EBI[0], BE, BEI[7], EI, BIE[4], BI],
CDE : [BCD[0], CD[1], CDG[4], DE, BEI[7], CE],
CDG : [DCG, CD[1], CDG[4], DG, CGD[0], CG[1]],
CDH : [DCH[8], CD[1], CDG[4], DH, CHG[3], CH],
CEF : [BCF[7], CE, BEF[9], EF[1], CFE[1], CF[0]],
CEG : [BCG[9], CE, BEI[7], EG[0], CGH[1], CG[1]],
CEH : [BCH[6], CE, BEI[7], EH, CHI[2], CH],
CGH : [GCH, CG[1], CGH[1], GH, CHG[3], CH],
]
三角形定理ループ
以下の定理を一つずつ試していって、何かが新しく明らかになったら、新しく明らかになるものが無くなるまで同じ定理をループする。そのループが終わり次第、また一番上の定理から始める。何も引っかからず、一番最後まで何も無かったら終了。
手元でtriangle、side、angleを更新していく。
- 1つの三角形の2角が同じであれば、その2角で共有していない2辺も同じ
- 1つの三角形の2辺が同じであれば、その2辺で共有していない2角も同じ
- 2つの三角形の2角が同じであれば、残り1角も同じ。更に対応する1辺が同じであれば、残りの2辺も同じ
- 2つの三角形の2辺とその間の角が同じであれば、残りの辺や角も同じ
- 3辺が同じであれば、対応する角も同じ
1つの三角形の2角。見つからなかった。
1つの三角形の2辺。
三角形。 結果。
CDG。 CDG[4] = CGD[0]。
見つかったのでもう1周。見つからない。
引っかかったので、一番上の定理に戻る。
1つの三角形の2角。
三角形。 結果。
ADI。 AD[0] = DI。
BEI。 BE = EI。
CDE。 DE = CE。
見つかったのでもう1周。見つからない。
これが一番上の定理なので、次の定理に進む。
1つの三角形の2辺。見つからない(厳密には見つかったが影響無し)。
2つの三角形の2角、更には対応する辺。1と6、1と8、6と8、2と6、という風に探していく。
三角形の対。 結果。
ADI、CDG。 ADG[7] = DCG。
引っかかったので、もう1回探す。見つからない。(考えてみれば、同じ定理では変更の影響がありそうな所だけ、調べれば良い)
一番上の定理に戻る。
1つの三角形の2角。見つからない。
1つの三角形の2辺。見つかったが影響無し。
2つの三角形の2角、更には対応する1辺。そもそも一番上の定理に行ってから変化してないので、今回も変化しないはず。
2つの三角形の2辺とその間の角。
三角形の対。 結果。
ABC、CEF。 HAI[8] = BEF[9]。AC = CE[3]。BCH[6] = BCF[7]。
見つかったので、もう1回(あー、これ、定理ごとも引っかかるたびにやり直した方が楽そうだな)。見つからない。
引っかかったので、一番上の定理に戻る。
1つの三角形の2角。見つかったら自動的にその定理を最初からやり直すことにした。
三角形。 結果。
ADH。 DH = AH。
CEH。 EH = CH。
一番上の定理なので、次に進む。
1つの三角形の2辺。見つからない。
2つの三角形の2角、更には対応する1辺。(この時点で、triangleを手元で自由に並び替えることにした。辞書方式なので多分OK。)見つからない。
2つの三角形の2辺とその間の角。見つからない。
2つの三角形の3辺。見つからない。
角の和
三角形定理ループが終わったんで、角の和を調べる。
点に着目して、まずは単純な角の和を調べる。文章内検索を使った。
着目した点。 結果。
A。 [6]DAH + [8]HAI = [0]DAI。
B。 [0]EBI + [1]CBI = 180。
C。 [6]DCG + GCH = [8]DCH。
C。 GCH + [6]BCH = [8]BCG。
C。 [6]BCH + [6]BCF = [3]FCH。
C。 [8]DCH + [6]BCH = [0]BCD。
C。 [8]BCG + [6]DCG = [0]BCD。
C。 [8]BCG + [6]BCF = [0]FCG。
C。 [3]FCH + GCH = [0]FCG。
C。 [0]BCD + [6]BCF = DCF。
C。 [0]FCG + [6]DCG = DCF。
D。 [6]ADG + [0]CDG = [1]ADC。
E。 [6]BEI + [8]BEF = [0]FEI。
G。 [0]CGD + [1]CGH = 180。
H。 [2]AHG + [3]CHG = 180。
I。 [0]AIH + [5]AIE = 180。
次に三角形に着目して、外角を調べた。
着目した三角形。 結果。
ABC。 [8]HAI + [6]BCH = [0]EBI。
CEG。 [8]BCG + [6]BEI = [0]CGD。
ADH。 [6]DAH + [6]ADG = [3]AHI。
CEH。 はADHと同じなんで省略。
ADI。 [0]DAI + [6]ADG = [5]AIE。
CDG。 [6]DCG + [0]CDG = [1]CGH。
BEI。 [0]EBI + [6]BEI = [5]BIH。
BEI。 [6]BEI + [0]BIE = [1]CBI。
AHI。 [8]HAI + [3]AHI = [5]BIH。
AHI。 [8]HAI + [0]AIH = [2]AHG。
CDH。 [8]DCH + [0]CDG = [2]AHG。
CGH。 GCH + [1]CGH = [2]CHI。
CGH。 GCH + [3]CHG = [0]CGD。
統合すると
[6] + [8] = [0]
[0] + [1] = 180
[6] + GCH = [8]
[6] + [6] = [3]
[3] + GCH = [0]
[0] + [6] = DCF
[6] + [0] = [1]
[2] + [3] = 180
[0] + [5] = 180
[0] + [6] = [5]
[8] + [3] = [5]
[8] + [0] = [2]
GCH + [1] = [2]
2つ同じであれば、残り1つも同じ。答えが同じで、残りどちらか1つが同じを探して、それから、答え以外の2つが同じを探す。
式の対。 結果。
[0] + [1] = 180、[0] + [5] = 180。 [1] = [5]。
[0] + [6] = DCF、[6] + [0] = [1]、[0] + [6] = [5]。 DCF = [1] = [5]。
変化があったんで、三角形定理ループを最初からやる。
1つの三角形の2角。見つからない。
1つの三角形の2辺。見つからない。
2つの三角形の2角と、あるなら対応する辺。見つからない。
2つの三角形の2辺と間の角。見つからない。
2つの三角形の3辺。見つからない。
じゃあ、問題文に戻って、答えなきゃいけないのは、「[8]HAI * result1 + [6]DAH * result2 = 180」。
ここからは人力になってしまうわけだけど、この3つの式を使う。
- [6] + [8] = [0]
- [6] + [0] = [1]
- [0] + [1] = 180
180 = ([6] + [8]) + ([6] + ([6] + [8])) = [6] * 3 + [8] * 2
つまり答えは、3と2。正解だ。やったー!