06年度トライアル問題 問題9
『図の四角形ABCDはAB=BC=CDで、角B=168度、角C=108度です。角Dの大きさを求めなさい。
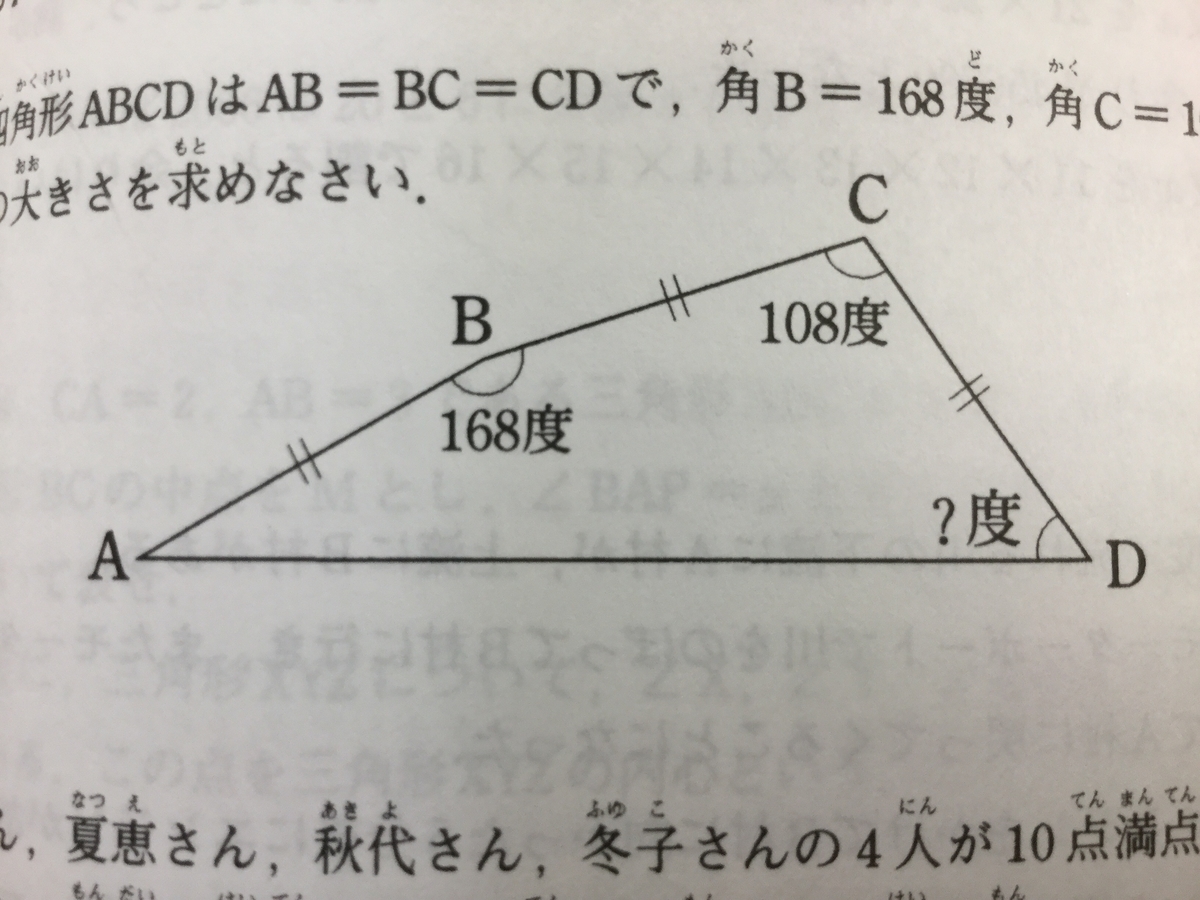 』
』
セットアップ
三角形を探して、角や辺のイコールを探して、それらを統合する。三角形定理ループに備える。
点に着目して三角形を探す。繋がっている点からも別の繋がっている点に繋がっていたら、三角形。
着目した点。繋がっている点。 見つかった三角形。
A。B、D。
B。C。
C。D。
D。
問題文のイコールを記述する。
イコールの辺。
AB、BC、CD。
対頂角も平行線の同位角や錯角も無し。
side := [
0 : [AB, BC, CD]
]
普段だったら三角形のリストとイコールのリストを統合する所だが、三角形のリストは無し。
三角形定理ループも、角や辺の和も無いんで、もうさっさと作図の段階に入る。
作図
以下4種類の作図をしていく。直接作図したもの以外に三角形や、あるいは正四角形や正五角形ができていたら、次の定理ループで角度が明らかになる可能性がある。
- 点と点を結んで線にする
- 点と点の距離の分だけ線を延長
- 2点と、その間の垂直線とどこか1辺の交点による、二等辺三角形の作図
- 同じ三角形を(同じ長さの辺の所に)作図
- 正四角形
- 正五角形
じゃあ、点と点を結んで線にする所から。
点Aを結ばれていない点Cと結ぶ。まだ基準がハッキリしないけど、新しく三角形を作ったから三角形定理ループにかけてみようか。
新しく作られた三角形を探す。辺ACに着目する。点Aだけに着目すれば良いかと思ったけど、辺ACに含まれる全ての点に着目した方が良い。
着目した点。繋がっている点。 見つけた三角形。
A。B、C、D。 ABC、ACD。
C。B、D。
triangle := [
ABC : [BAC, AB, ABC, BC, ACB, AC],
ACD : [CAD, AC, ACD, CD, ADC, AD]
]
新しく生まれた定義や対頂角や平行線をイコールのリストに登録する。特に無し。
三角形とイコールのリストを統合する。これでセットアップは完了。
triangle := [
ABC : [BAC, AB[0], ABC, BC[0], ACB, AC],
ACD : [CAD, AC, ACD, CD[0], ADC, AD]
]
三角形定理ループにかける。
1つの三角形に2つの同じ角。ある。
三角形。 結果。
ABC。 BAC = ACB。
angle := [
0 : [BAC, ACB]
]
1つの三角形に2つの同じ辺。ある、が既に対応済み。
2つの三角形の2つの角が同じ、更には対応する1辺が同じ。無い。
2つの三角形の2辺とその間の角が同じ。無い。
2つの三角形の3辺が同じ。無い。
角の和と辺の和の段階に入る。
単純な角の和。点に着目して発見する。
着目した点。 角の和。
A。 BAC[0] + CAD = BAD。
C。 ACB[0] + ACD = BCD。
三角形の外角。三角形に着目する。しかし、外角が発生するような三角形は無し。
式の2つが同じだったら残りの1つも同じだが、無し。
辺の和も無し。
っと、ここで気付いたが、168°だとか実際の数字が出てくると、内角が合計180°というのも考えるべきだな。
「角1 + 角2 + 角3 = 180」という式で表すか。
BAC[0] + ABC + ACB[0] = 180
CAD + ACD + ADC = 180
いやしかもABC = 168なのか。
angle := [
0 : [BAC, ACB, 6],
1 : [ABC, 168],
2 : [BCD, 108]
]
こんな感じの表記で良いだろうか。
そうすると、
[0] + CAD = BAD
[0] + ACD = [2]
6 + ACD = 108、ACD = 102
angle := [
0 : [BAC, ACB, 6],
1 : [ABC, 168],
2 : [BCD, 108],
3 : [ACD, 102]
]
CAD + ACD[3] + ADC = 180
まあでもこんなもんか。
triangle := [
ABC : [BAC[0], AB[0], ABC[1], BC[0], ACB[0], AC],
ACD : [CAD, AC, ACD[3], CD[0], ADC, AD]
]
三角形定理ループにかけても特に影響無し。
判明したものが辺ACに関するものばかりだったんで、この作図には意味が無かった。
ちょっと初めてだったんでゴチャゴチャした。休憩(2回目)。
じゃあ次は、点BとDを結ぶ。
着目した点。繋がっている点。 発見した三角形。
B。A、C、D。 ABD、BCD。
D。A、C。
triangle := [
ABD : [BAD, AB, ABD, BD, ADB, AD],
BCD : [CBD, BC, BCD, CD, BDC, BD]
]
新しく追加された定義や対頂角や平行線は無し。
元々のイコールのリストと統合。
triangle := [
ABD : [BAD, AB[0], ABD, BD, ADB, AD],
BCD : [CBD, BC[0], BCD, CD[0], BDC, BD]
]
これでセットアップは完了。
三角形定理ループにかける。
1つの三角形の2角が同じ。無い。
1つの三角形の2辺が同じ。ある。
三角形。 結果。
BCD。 CBD = BDC。
ああ、そうだ、実際の数字とのイコールも登録しておくんだった。
angle := [
0 : [CBD, BDC],
1 : [ABC, 168],
2 : [BCD, 108]
]
最初に戻って、1つの三角形の2角が同じ。あるが対応済み。
1つの三角形の2辺が同じ。あるが対応済み。
2つの三角形の2角が同じ、更には対応する1辺が同じ。無い。
2つの三角形の2辺とその間の角が同じ。無い。
2つの三角形の3辺が同じ。無い。
角の和と辺の和の段階に入る。
単純な角の和。
着目した点。 角の和。
B。 ABD + CBD[0] = ABC[1]。
D。 BDC[0] + ADB = ADC。
三角形の内角や外角。
着目した三角形。 角の和。
ABD。 BAD + ABD + ADB = 180。
ABD。 BAD + ADB = CBD[0]。
BCD。 CBD[0] + BCD[2] + BDC[0] = 180。
BCD。 BCD[2] + BDC[0] = ABD。
統合する。[1] = 168、[2] = 108。
ABD + [0] = 168
[0] + ADB = ADC
BAD + ADB = [0]
108 + [0] = ABD
BAD + ABD + ADB = 180
[0] + 108 + [0] = 180
「[0] + 108 + [0] = 180」より、[0] = 36。
うーん、しかしそうすると、「ABD + 36 = 168」と「108 + 36 = ABD」で矛盾が出るな。
いや、この問題は2ステップの作図が必要で、このままだと膨大な作業量になってしまうので、部分的にでも自動化を模索したい。今回はここで切る。