算数オリンピック13年度トライアル問題 問題10
『図の四角形ABCDで、点E、F、G、H、MはAE : EB = AF : FD = 2 : 5、BG : GH : HC = 3 : 2 : 2、CM = DMを満たす辺上の点です。いま、EG、FH上にそれぞれEP = PG、FQ = QHとなる点P、Qをとるとき、PQ = BMを求めなさい。
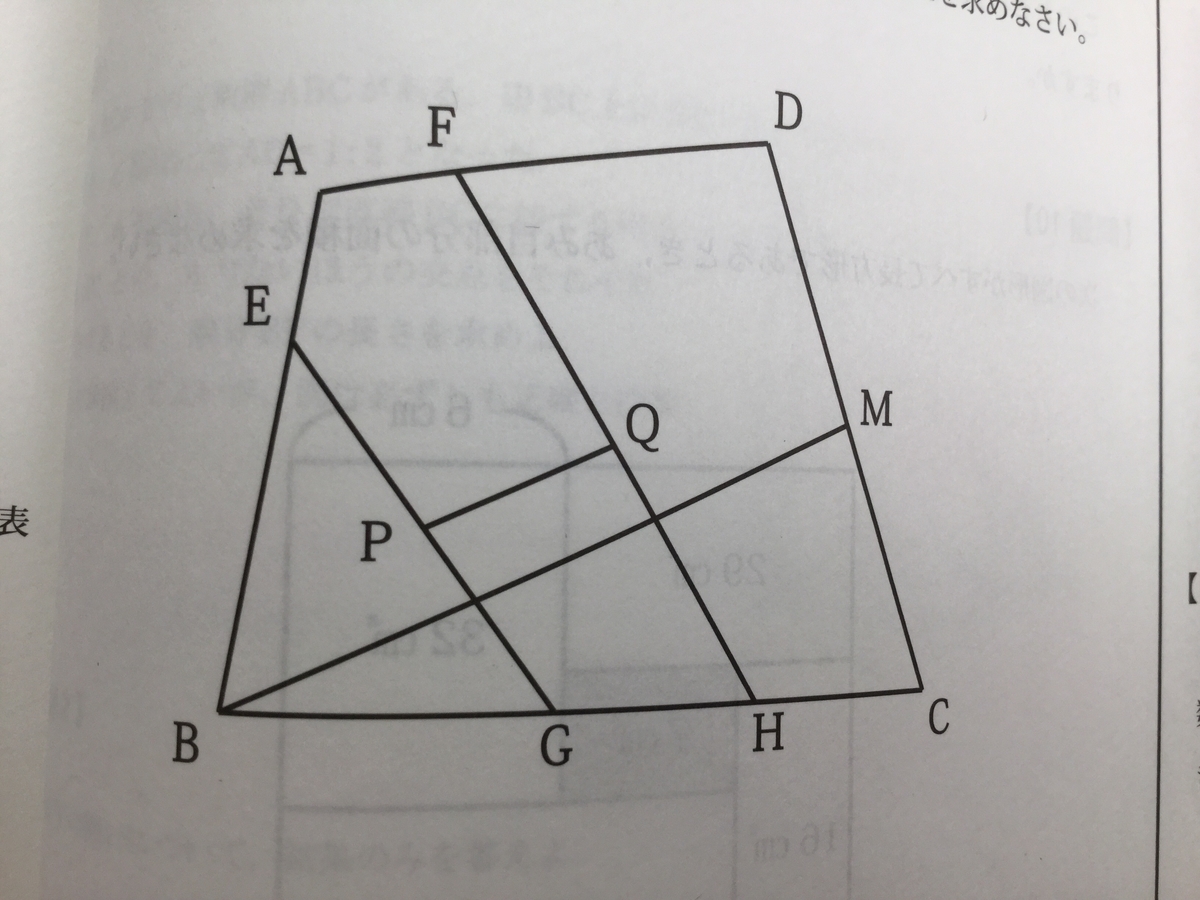 』
』
名付けられていない交点は、上からR、Sと名付ける。
graph := [
A : [
[[F, D], []],
[[E, B], []]
]
,
B : [
[[E, A], []],
[[S, R, M], []],
[[G, H, C], []]
]
,
C : [
[[B, G, H], []],
[[D, M], []]
]
,
D : [
[[A, F], []],
[[M, C], []]
]
,
E : [
[[A], [B]],
[[P, S, G], []]
]
,
F : [
[[A], [D]],
[[Q, R, H], []]
]
,
G : [
[[B], [H, C]],
[[E, P, S], []]
]
,
H : [
[[B, G], [C]],
[[F, Q, R], []]
]
,
M : [
[[D], [C]],
[[B, S, R], []]
]
,
P : [
[[E], [S, G]],
[[Q], []]
]
,
Q : [
[[P], []],
[[F], [R, H]]
]
,
R : [
[[F, Q], [H]],
[[B, S], [M]]
]
,
S : [
[[E, P], [G]],
[[B], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
];
cluster_lst := [
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
}じゃあ、ここからスタート。クラスタは、前回と同じく最初は登録しない。
辺の和を登録する。
辺を区切ることによる180°の角の和も登録する。
平行線リストを見て、角のイコールも登録する。
三角形も登録する。graphの点と繋がっている点が更に別の繋がっている点と繋がっていたら、三角形。
辺を区切ることによる180°の角の和を登録することで、対頂角のイコールは自動的に弾き出されるし、三角形の外角も自動的に弾き出される。
graph := [
A : [
[[F, D], []],
[[E, B], []]
]
,
B : [
[[E, A], []],
[[S, R, M], []],
[[G, H, C], []]
]
,
C : [
[[B, G, H], []],
[[D, M], []]
]
,
D : [
[[A, F], []],
[[M, C], []]
]
,
E : [
[[A], [B]],
[[P, S, G], []]
]
,
F : [
[[A], [D]],
[[Q, R, H], []]
]
,
G : [
[[B], [H, C]],
[[E, P, S], []]
]
,
H : [
[[B, G], [C]],
[[F, Q, R], []]
]
,
M : [
[[D], [C]],
[[B, S, R], []]
]
,
P : [
[[E], [S, G]],
[[Q], []]
]
,
Q : [
[[P], []],
[[F], [R, H]]
]
,
R : [
[[F, Q], [H]],
[[B, S], [M]]
]
,
S : [
[[E, P], [G]],
[[B], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△BES : [EBS, BE, BEP, ES, BSE, BS],
△BEG : [EBS, BE, BEP, EG, BGE, BG],
△BGS : [GBS, BG, BGE, GS, BSE, BS],
△BHR : [GBS, BH, BHF, HR, BRH, BR],
△BCM : [GBS, BC, BCD, CM, BMC, BM]
];
cluster_lst := [
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
AE + BE == AB;
AF + DF == AD;
BG + GH == BH;
BG + CG == BC;
BH + CH == BC;
GH + CH == CG;
DM + CM == CD;
EP + PS == ES;
EP + GP == EG;
FQ + QR == FR;
FQ + HQ == FH;
FR + HR == FH;
QR + HR == QH;
BR + MR == BM;
RS + MR == MS;
ES + GS == EG;
PS + GS == GP;
BS + RS == BR;
BS + MS == BM;
AEP_p + BEP_p == AEB_h; #180と登録した方が良かったかな
AFQ_p + DFQ_p == AFD_h;
BGE_p + EGH_p == BGH_h;
BHF_p + CHF_p == BHC_h;
BMD_p + BMC_p == CMD_h;
EPQ_p + QPS_p == EPS_h;
FQP_p + PQR_p == FQR_h;
BRF_p + BRH_p == FRH_h;
FRM_p + HRM_p == FRH_h;
BRF_p + FRM_p == BRM_h;
BRH_p + HRM_p == BRM_h;
BSE_p + BSG_p == ESG_h;
ESR_p + GSR_p == ESG_h;
BSE_p + ESR_p == BSR_h;
BSG_p + GSR_p == BSR_h;
}で、ここで気付いたけど、この後どうやっても、この三角形BCEとBCMの外でクラスタが登録されることは無い。だから、ABCDをクラスタとして登録してみることにした。
前回と同じく、作業手順を示す、大雑把な思考過程というか。クラスタの点を更新したら、基本的に角や辺は考え直している。
[[A, B, C, D], [EAF, AB, EBG, BC, BCD, CD, ADM, AD]]
AE + BE == AB; E EG
AF + DF == AD; F FH
BG + CG == BC; G
BH + CH == BC; H
DM + CM == CD; M BM
[[A, B, C, D], [EAF, AB, EBG, BC, BCD, CD, ADM, AD]]
AE + BE == AB;
BG + CG == BC;
EG
[[A, E, G, C, D], [EAF, AE, AEP, EG, EGH, CG, BCD, CD, ADM, AD]]
[[E, B, G], [BEP, BE, EBG, BG, BGE, EG]]
[[A, B, C, D], [EAF, AB, EBG, BC, BCD, CD, ADM, AD]]
AF + DF == AD;
BH + CH == BC;
FH
[[A, B, H, F], [EAF, AB, EBG, BH, BHF, FH, AFQ, AF]]
[[F, H, C, D], [DFQ, FH, BHF, CH, BCD, CD, ADM, DF]]
[[A, B, C, D], [EAF, AB, EBG, BC, BCD, CD, ADM, AD]]
DM + CM == CD;
BM
[[A, B, M, D], [EAF, AB, EBS, BM, BMD, DM, ADM, AD]]
[[B, M, C], [GBS, BM, BMC, CM, BCD, BC]] #手順において混乱がある
で、交点を考えなければいけないわけだが、一晩考えたんだが、三角関数を導入することにする。
でその前に、三角形の三辺が同じであれば合同は、俺はあの自分の考え方でも良いような気もしているが、しかし確かに厳密では無いかもしれない。
その場合は、まず角の二等分線の作図から、二等辺三角形の二辺が同じであればその底の方の二角も同じを証明する。まあ、二等分線を作図して、同じ長さの1辺とその共有する1辺とその間の角が同じだから合同をやる。
で、底辺から同じ長さの2辺が伸びているが角度は違うものを仮定して、その2つの三角形の頂点を結ぶ。そうすると二つの二等辺三角形ができるが、それぞれの角がイコールなはずなのに、片方はもう一方に含まれるのに、もう片方はもう一方を含むということになって、矛盾するので2辺が同じであれば角度も同じということになる。
で、平行四辺形の底辺が同じであれば上の方は平行移動しても面積は同じの証明をして、そこから有名なピタゴラスの定理の証明をすれば良いだろう。
角度による辺の長さの割合の計算は、厳密にはどうすれば良いかは分からないが、とにかく三角形が定まれば辺や角の大きさを出すような、データやちょっとした対応付けを、ここでは三角関数と呼ぶことにしよう(wikipediaを見てみたら、この呼び名で合っているようだ)。
で、平面という概念を導入するかだが、前に言った、平面において1点から伸びる3辺があって、2辺のポジティブな角が、他2つの組み合わせのポジティブ角以上であれば、それがその2つの角の和になるみたいなことは、よく考えたらそんなことは無かった。大体角の大きさが同じな3辺を想像すれば良い。
だから、平面という概念を想定する利点があるとしたら、今の所は三角関数が成立するということだけだ。クラスタの外側から作図する時に、必要になる気もするが。
後は、クラスタについても少し考えた。ネガティブな角を含むクラスタの話だけど、よく考えたら2つの辺が繋がっている時に、ポジティブな角で繋がっているのかネガティブな角で繋がっているのかは分からない、というかどちらでもある。だからクラスタとは、辺の繋がりでは無く、その内側の面のことで、だから三角形を基礎に考えるのは正しいし、また面として確保されてなければならないという意味で、ネガティブな角を含むクラスタを考えるのは良くないんじゃないかと思う。
クラスタの交点に戻る。
クラスタな。[A, B, C, D]では無く、[A, E, B, G, H, C, M, D, F]と考えることができれば、交点ができるかだけなら判断は簡単なんだけどな。
例えば、EGとFHとBMの場合、EGとFHは循環リストで考えても、お互いに跨っていない。別にあるか、あるいは完全に覆っているか。こういう場合は交点はできない。
EGとBMなんかは分かりやすくて、循環リストで考えても、お互いに跨っている。こういう場合は交点ができる。
EGとBM、FHとBMで交点ができるとして、BMにできたその二つの交点の位置関係はどうやって考えれば良いだろうか。こういう2点それぞれの位置関係が分かれば、全てにおいて位置関係が分かるはずだと思うが、表記的にも。
[A, E, B, G, H, C, M, D, F]を、[B, G, H, C, M, D, F, A, E]と循環させてみて思うに、EGとFHのどちらかがどちらかを覆わないように配置して、それぞれが含んでいるBかMの方に点ができる、という考え方はどうだろうか。
問題は、例えばEGとFHも互い違いになっている場合だろう。
3辺のそれぞれ2点を、X、Y、Zで考えてみる。[X, Y, X, Y]が互い違いになっている状態、循環しても意味は変わらない。ここにXを2つ入れてみる。[X, Z, Y, Z, X, Y]と入れても、[X, Z, Y, X, Z, Y]と入れても、いや、前者は1つと3つを挟むパターンであり、後者は2つと2つを挟むパターンと言えるだろう。この2通りについて考えてみる。
まず[X, Z, Y, Z, X, Y]のパターン。手元で描いてみて分かったが、このパターンは[Z, Y, Z, X, Y, X]であって、Yの挟んだ側にZとの交点ができて、YのXとの交点はXが挟んだ側にできる。
次に[X, Z, Y, X, Z, Y]のパターン。これが内側に三角形ができるパターンで、厄介なんだよな。抽象化するなら円の内側に3本の辺という感じだけど。Zの辺があるとして、その一方から、三角形を作るとして隣り合う2つの辺でどちらが短くて済むか、三角関数で調べるしか無いんじゃないかなあ。X、Y、Zのそれぞれの2点の端の6通りで試して、どれか一つでも明らかになれば、位置関係はハッキリするんだが。よく考えたら、角を挟む場合が厄介なんだよな、三角形が作れないから。
ああ、あるいは、区切られた1本の辺の対でどちらが短いか、か?
まあ今回は前者であって、[A, E, B, G, H, C, M, D, F]はEG・FH・BMでは[E, B, G, H, M, F]なので、BMのB側にEGと交点ができて、M側にFHと交点ができるわけだ。って、今回は作図じゃないから、もうできてるのか。
クラスタは、これからは間の点も全部含むことにしよう。そっちの方が分かりやすいから。じゃあ今日は、もうこれで良いかな。