算数オリンピック13年度トライアル問題 問題10
『図の四角形ABCDで、点E、F、G、H、MはAE : EB = AF : FD = 2 : 5、BG : GH : HC = 3 : 2 : 2、CM = DMを満たす辺上の点です。いま、EG、FH上にそれぞれEP = PG、FQ = QHとなる点P、Qをとるとき、PQ = BMを求めなさい。
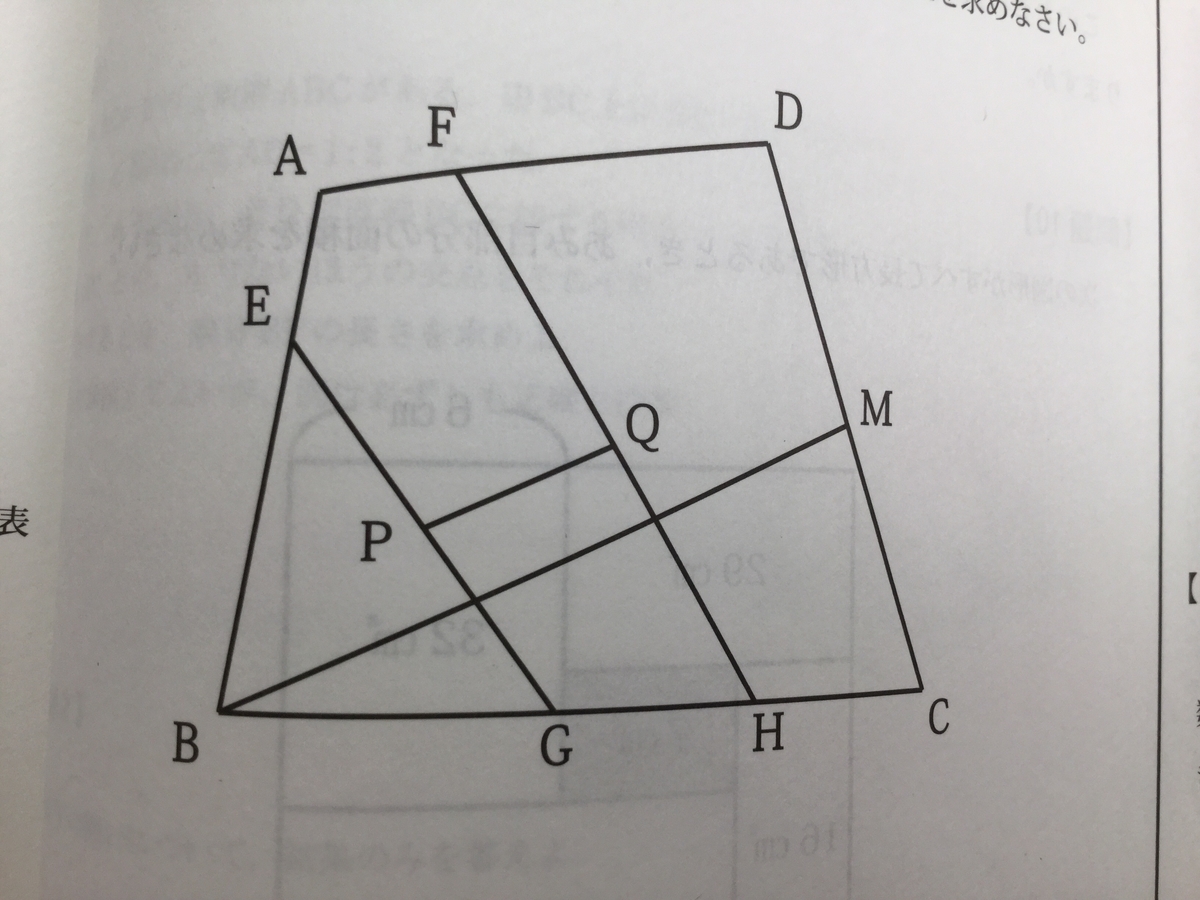 』
』
昨日の続きで、今日はクラスタに直線の点も入れて同じ作業をする。
名付けられていない交点は、上からR、Sと名付ける。今回は、最初から全体をクラスタとして登録する。
graph := [
A : [
[[F, D], []],
[[E, B], []]
]
,
B : [
[[E, A], []],
[[S, R, M], []],
[[G, H, C], []]
]
,
C : [
[[B, G, H], []],
[[D, M], []]
]
,
D : [
[[A, F], []],
[[M, C], []]
]
,
E : [
[[A], [B]],
[[P, S, G], []]
]
,
F : [
[[A], [D]],
[[Q, R, H], []]
]
,
G : [
[[B], [H, C]],
[[E, P, S], []]
]
,
H : [
[[B, G], [C]],
[[F, Q, R], []]
]
,
M : [
[[D], [C]],
[[B, S, R], []]
]
,
P : [
[[E], [S, G]],
[[Q], []]
]
,
Q : [
[[P], []],
[[F], [R, H]]
]
,
R : [
[[F, Q], [H]],
[[B, S], [M]]
]
,
S : [
[[E, P], [G]],
[[B], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
];
cluster_lst := [
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
}今回はここからスタート。
で、graphを見て、辺の和と、180度の角の和を登録する。
平行線リストを見て、平行線による角のイコールも登録する。
三角形も登録する。graphを見て、点と繋がっている点と点が繋がっていたら、三角形。
graph := [
A : [
[[F, D], []],
[[E, B], []]
]
,
B : [
[[E, A], []],
[[S, R, M], []],
[[G, H, C], []]
]
,
C : [
[[B, G, H], []],
[[D, M], []]
]
,
D : [
[[A, F], []],
[[M, C], []]
]
,
E : [
[[A], [B]],
[[P, S, G], []]
]
,
F : [
[[A], [D]],
[[Q, R, H], []]
]
,
G : [
[[B], [H, C]],
[[E, P, S], []]
]
,
H : [
[[B, G], [C]],
[[F, Q, R], []]
]
,
M : [
[[D], [C]],
[[B, S, R], []]
]
,
P : [
[[E], [S, G]],
[[Q], []]
]
,
Q : [
[[P], []],
[[F], [R, H]]
]
,
R : [
[[F, Q], [H]],
[[B, S], [M]]
]
,
S : [
[[E, P], [G]],
[[B], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△BES : [EBS, BE, BEP, ES, BSE, BS],
△BEG : [EBS, BE, BEP, EG, BGE, BG],
△BGS : [GBS, BG, BGE, GS, BSE, BS],
△BHR : [GBS, BH, BHF, HR, BRH, BR],
△BCM : [GBS, BC, BCD, CM, BMC, BM]
];
cluster_lst := [
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
AE + BE == AB;
AF + DF == AD;
BG + GH == BH;
BG + CG == BC;
BH + CH == BC;
GH + CH == CG;
DM + CM == CD;
EP + PS == ES;
EP + GP == EG;
FQ + QR == FR;
FQ + HQ == FH;
FR + HR == FH;
QR + HR == QH;
BR + MR == BM;
RS + MR == MS;
ES + GS == EG;
PS + GS == GP;
BS + RS == BR;
BS + MS == BM;
AEP_p + BEP_p == AEB_h;
AFQ_p + DFQ_p == AFD_h;
BGE_p + EGH_p == BGH_h;
BHF_p + CHF_p == BHC_h;
BMD_p + BMC_p == CMD_h;
EPQ_p + QPS_p == EPS_h;
FQP_p + PQR_p == FQR_h;
BRF_p + BRH_p == FRH_h;
FRM_p + HRM_p == FRH_h;
BRF_p + FRM_p == BRM_h;
BRH_p + HRM_p == BRM_h;
BSE_p + BSG_p == ESG_h;
ESR_p + GSR_p == ESG_h;
BSE_p + ESR_p == BSR_h;
BSG_p + GSR_p == BSR_h;
}
昨日と同じように、クラスタからクラスタを弾き出す。思考過程を晒す。今回は点だけに着目して、graphでクラスタ内でクラスタ以外の方法で繋がっているものを探していった。
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
BM
EG
FH
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
BM
[[B, G, H, C, M], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, BM]
[[A, E, B, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BM, BMD_p, DM, ADM_p, DF, AFD_h, AF]]
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
EG
[[A, E, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EG, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
[[E, B, G], [BEP_p, BE, EBG_p, BG, BGE_p, EG]]
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
FH
[[H, C, M, D, F], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FH]]
[[A, E, B, G, H, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, FH, AFQ_p AF]]
いや、本当は、交点の判定を先にするべきなのだろうな。
[A, E, B, G, H, C, M, D, F]
BM
EG
FH
[E, B, G, H, M, F]
BMには、B側にEG、M側にFH
EGとFHにBMと一つずつ
B : [
[[S, R, M], ],
]
M : [
[[B, S, R], ]
]
R : [
[[B, S], [M]]
]
S : [
[[B], [R, M]]
]
E : [
[[P, S, G], ]
]
G : [
[[E, P, S], ]
]
S : [
[[E, P], [G]],
]
F : [
[[Q, R, H], ]
]
H : [
[[F, Q, R], ]
]
R : [
[[F, Q], [H]],
]
PとS、QとRの位置関係はどう考えよう。
分からないのではないか?そうすると、どうしよう。
前者のPとSのケースについて考えてみる。
E : [
[[P, S, G], ]
]
G : [
[[E, P, S], ]
]
S : [
[[E, P], [G]],
]
P : [
[[E], [S, G]],
]
んー、こう考えてみるか?
E : [
[[P, S, G], ]
]
G : [
[[E, P, S], ]
]
S : [
[[E], [G]],
]
P : [
[[E], [G]],
]
修正前だと、E→P→S→G、あるいはG→S→P→Eが可能。修正後だと、E→S→、の後がGにおいてはE・P・Sなので続かない。そういう場合は無視すべきか?
あるいは、
E : [
[[P, S, G], , ]
]
G : [
[[E, P, S], , ]
]
S : [
[[E], [P], [G]],
]
P : [
[[E], [S], [G]],
]
一方から見て位置関係がどちらか分からないということは、もう一方からも分からないということではないか。
いやどうだろう、これは昔考えた「位置の制約」に近いのではないか。
EG ~ @{E < G, P, S}
EG ~ @{E, P, S < G}
EG ~ @{E < P < G}
EG ~ @{E < S < G}
だっけか?忘れたけど。
そういうものが確定しないと交点を認めないというスタンスでは、この問題のクラスタを取得し切ることはできない。1番目と2番目と3番目(位置の制約)について、2番目と3番目は本質的に同じだとして、1番目を試して駄目だったら、2番目を試すことにしよう。というか3番目は、できればこれ以上話をややこしくしたくない。
まあでもこれは、初期段階ならこの判断はいらないし、作図段階なら、更に少し作図して三角関数で素直に判定した方が良いのかもしれない。分からないなら本当にどちらか分からない状態なわけで、そんな状態でそういう機能で交点を考えるのに何の旨味があるのかというか。
一晩開けて思うのだけど、1番目と2番目は、大は小を兼ねるというか、2番目の真ん中を消せば1番目になるから、とりあえず2番目にしてみようかな。
そもそも交点を作らないというのが元々だったんだけど、そうするとクラスタEAFRSを考えることができなくなる。そういう順番が関わるみたいなのは、できれば避けたい。失敗し次第、その交点を作らない方針に戻すとして、だからとりあえず2番目で行こう。
まあ、今回は、そもそも作図で無く初期のセットアップだから、やり直さずこのまま続けるが。
BMの間は、B、S、R、M。BS, BSR_h, RS, BRM_h, MR。
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]]
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]]
EGの間は、E、P、S、G。EP, EPS_h, PS, ESG_h, GS。
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
[[E, B, G, S, P], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]]
FHの間は、F、Q、R、H。FQ, FQR_h, QR, FRH_h, HR
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]]
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]]
graph := [
A : [
[[F, D], [], []],
[[E, B], [], []]
]
,
B : [
[[E, A], [], []],
[[S, R, M], [], []],
[[G, H, C], [], []]
]
,
C : [
[[B, G, H], [], []],
[[D, M], [], []]
]
,
D : [
[[A, F], [], []],
[[M, C], [], []]
]
,
E : [
[[A], [], [B]],
[[P, S, G], [], []]
]
,
F : [
[[A], [], [D]],
[[Q, R, H], [], []]
]
,
G : [
[[B], [], [H, C]],
[[E, P, S], [], []]
]
,
H : [
[[B, G], [], [C]],
[[F, Q, R], [], []]
]
,
M : [
[[D], [], [C]],
[[B, S, R], [], []]
]
,
P : [
[[E], [], [S, G]],
[[Q], [], []]
]
,
Q : [
[[P], [], []],
[[F], [], [R, H]]
]
,
R : [
[[F, Q], [], [H]],
[[B, S], [], [M]]
]
,
S : [
[[E, P], [], [G]],
[[B], [], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△BES : [EBS, BE, BEP, ES, BSE, BS],
△BEG : [EBS, BE, BEP, EG, BGE, BG],
△BGS : [GBS, BG, BGE, GS, BSE, BS],
△BHR : [GBS, BH, BHF, HR, BRH, BR],
△BCM : [GBS, BC, BCD, CM, BMC, BM]
];
cluster_lst := [
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]],
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, G, S, P], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]],
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]]
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
AE + BE == AB;
AF + DF == AD;
BG + GH == BH;
BG + CG == BC;
BH + CH == BC;
GH + CH == CG;
DM + CM == CD;
EP + PS == ES;
EP + GP == EG;
FQ + QR == FR;
FQ + HQ == FH;
FR + HR == FH;
QR + HR == QH;
BR + MR == BM;
RS + MR == MS;
ES + GS == EG;
PS + GS == GP;
BS + RS == BR;
BS + MS == BM;
AEP_p + BEP_p == AEB_h;
AFQ_p + DFQ_p == AFD_h;
BGE_p + EGH_p == BGH_h;
BHF_p + CHF_p == BHC_h;
BMD_p + BMC_p == CMD_h;
EPQ_p + QPS_p == EPS_h;
FQP_p + PQR_p == FQR_h;
BRF_p + BRH_p == FRH_h;
FRM_p + HRM_p == FRH_h;
BRF_p + FRM_p == BRM_h;
BRH_p + HRM_p == BRM_h;
BSE_p + BSG_p == ESG_h;
ESR_p + GSR_p == ESG_h;
BSE_p + ESR_p == BSR_h;
BSG_p + GSR_p == BSR_h;
}
いろいろ考察したんで、一旦表示した。続きをする。
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]]
GS
HR
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]]
GS
[[B, G, S], [GBS_p, BG, BGE_p, GS, BSG_p, BS]]
[[G, H, C, M, R, S], [EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, GSR_p, GS]]
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]]
HR
[[B, G, H, R, S], [GBS_p, BG, BGH_h, GH, BHF_p, RH, BRH_p, RS, BSR_h, BS]]
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]]
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]]
ES
FR
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]]
ES
[[A, E, S, R, M, D, F], [EAF_p, AE, AEP_p, ES, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]]
[[E, B, S], [BEP_p, BE, EBS_p, BS, BSE_p, ES]]
ES。E, P, S。EP, EPS_h, PS
[[A, E, S, R, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]]
[[E, B, S], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]]
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]]
FR
[[A, E, B, S, R, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, FR, AFQ_p, AF]]
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FR]]
FR。F、Q、R。FQ, FQR_h, QR。
[[A, E, B, S, R, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]]
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR]]
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
MS
FH
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
MS
[[A, E, P, S, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, MS, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[S, G, H, C, M], [GSR_p, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MS]],
MS。M、R、S。MR, BRM_h, RS
[[A, E, P, S, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[S, G, H, C, M], [GSR_p, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS]],
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
FH
[[A, E, P, S, G, H, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, FH, AFQ_p, AF]],
[[H, C, M, D, F], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FH]],
FH。F、Q、R、H。FQ, FQR_h, QR, FRH_h, HR。
[[A, E, P, S, G, H, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
[[H, C, M, D, F], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[E, B, G, S, P], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]]
BS
[[E, B, S, P], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]]
[[B, G, S], [GBS_p, BG, BGE_p, GS, BSG_p, BS]]
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
MR
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[M, D, F, Q, R], [BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRM_p, MR]],
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]]
EG
BR
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]]
EG
[[A, E, G, H, R, Q, F], [EAF_p, AE, AEP_p, EG, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]]
[[E, B, G], [BEP_p, BE, EBG_p, BG, BGE_p, EG]]
EG。E, P, S, G。EP, EPS_h, PS, ESG_h, GS。
[[A, E, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]]
[[E, B, G], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]]
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]]
BR
[[A, E, B, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BR, BRF_p, QR, FQR_h, FQ, AFQ_p AF]]
[[B, G, H, R], [GBS_p, BG, BGH_h, GH, BHF_p, HR, BRH_p, BR]]
graph := [
A : [
[[F, D], [], []],
[[E, B], [], []]
]
,
B : [
[[E, A], [], []],
[[S, R, M], [], []],
[[G, H, C], [], []]
]
,
C : [
[[B, G, H], [], []],
[[D, M], [], []]
]
,
D : [
[[A, F], [], []],
[[M, C], [], []]
]
,
E : [
[[A], [], [B]],
[[P, S, G], [], []]
]
,
F : [
[[A], [], [D]],
[[Q, R, H], [], []]
]
,
G : [
[[B], [], [H, C]],
[[E, P, S], [], []]
]
,
H : [
[[B, G], [], [C]],
[[F, Q, R], [], []]
]
,
M : [
[[D], [], [C]],
[[B, S, R], [], []]
]
,
P : [
[[E], [], [S, G]],
[[Q], [], []]
]
,
Q : [
[[P], [], []],
[[F], [], [R, H]]
]
,
R : [
[[F, Q], [], [H]],
[[B, S], [], [M]]
]
,
S : [
[[E, P], [], [G]],
[[B], [], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△BES : [EBS, BE, BEP, ES, BSE, BS],
△BEG : [EBS, BE, BEP, EG, BGE, BG],
△BGS : [GBS, BG, BGE, GS, BSE, BS],
△BHR : [GBS, BH, BHF, HR, BRH, BR],
△BCM : [GBS, BC, BCD, CM, BMC, BM]
];
cluster_lst := [
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]],
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, G, S, P], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]],
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]],
[[B, G, S], [GBS_p, BG, BGE_p, GS, BSG_p, BS]],
[[G, H, C, M, R, S], [EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, GSR_p, GS]],
[[B, G, H, R, S], [GBS_p, BG, BGH_h, GH, BHF_p, RH, BRH_p, RS, BSR_h, BS]],
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[A, E, S, R, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, S], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]],
[[A, E, B, S, R, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]],
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR]]
[[A, E, P, S, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[S, G, H, C, M], [GSR_p, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS]],
[[A, E, P, S, G, H, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
[[H, C, M, D, F], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[E, B, S, P], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]],
[[M, D, F, Q, R], [BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRM_p, MR]],
[[A, E, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
[[E, B, G], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]],
[[A, E, B, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BR, BRF_p, QR, FQR_h, FQ, AFQ_p AF]],
[[B, G, H, R], [GBS_p, BG, BGH_h, GH, BHF_p, HR, BRH_p, BR]]
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
AE + BE == AB;
AF + DF == AD;
BG + GH == BH;
BG + CG == BC;
BH + CH == BC;
GH + CH == CG;
DM + CM == CD;
EP + PS == ES;
EP + GP == EG;
FQ + QR == FR;
FQ + HQ == FH;
FR + HR == FH;
QR + HR == QH;
BR + MR == BM;
RS + MR == MS;
ES + GS == EG;
PS + GS == GP;
BS + RS == BR;
BS + MS == BM;
AEP_p + BEP_p == AEB_h;
AFQ_p + DFQ_p == AFD_h;
BGE_p + EGH_p == BGH_h;
BHF_p + CHF_p == BHC_h;
BMD_p + BMC_p == CMD_h;
EPQ_p + QPS_p == EPS_h;
FQP_p + PQR_p == FQR_h;
BRF_p + BRH_p == FRH_h;
FRM_p + HRM_p == FRH_h;
BRF_p + FRM_p == BRM_h;
BRH_p + HRM_p == BRM_h;
BSE_p + BSG_p == ESG_h;
ESR_p + GSR_p == ESG_h;
BSE_p + ESR_p == BSR_h;
BSG_p + GSR_p == BSR_h;
}
えー、続き。該当するものだけ表示することにする。
[[G, H, C, M, R, S], [EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, GSR_p, GS]],
HR
[[G, H, R, S], [EGH_p, GH, BHF_p, HR, BHR_p, RS, GSR_p, GS]],
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[A, E, S, R, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
FR
[[A, E, S, R, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, FR, AFQ_p, AF]],
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FR],
FR。F, Q, R。FQ, FQR_p, QR
[[A, E, S, R, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_p, FQ, AFQ_p, AF]],
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_p, QR],
[[A, E, B, S, R, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]],
ES
[[A, E, S, R, F], [EAF_p, AE, AEP_p, ES, ESR_p, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]],
[[E, B, S], [BEP_p, BE, EBS_p, BS, BSE_p, ES]],
ES。E, P, S。EP, EPS_p, PS
[[A, E, S, R, F], [EAF_p, AE, AEP_p, EP, EPS_p, PS, ESR_p, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]],
[[E, B, S], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_p, EP]],
[[A, E, P, S, R, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
FR
[[A, E, P, S, R, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, FR, AFQ_p, AF]],
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFR_p, FR]],
FR。FQ, FQR_p, QR
[[A, E, P, S, R, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_p, FQ, AFQ_p, AF]],
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFR_p, FQ, FQR_p, QR]],
[[S, G, H, C, M, R], [GSR_p, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS]],
HR
[[S, G, H, R], [GSR_p, GS, EGH_p, GH, BHF_p, HR, BRH_p, RS]],
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
PQ
RS
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
PQ
[[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP_p, FQ, AFQ_p, AF]],
[[P, S, G, H, R, Q], [QPS_p, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, PQR_p, PQ]],
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
RS
[[A, E, P, S, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_h, FQ, AFQ_p, AF]],
[[S, G, H, R], [GSR_p, GS, EGH_p, GH, BHF_p, HR, BRH_p, RS]],
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
MR
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[M, D, F, Q, R], [BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRM_p, MR]],
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
PQ
RS
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
PQ
[[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP_p, FQ, AFQ_p, AF]],
[[P, S, G, H, R, Q], [QPS_p, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, PQR_p, PQ]],
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
RS
[[A, E, P, S, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_h, FQ, AFQ_p, AF]],
[[S, G, H, R], [GSR_p, GS, EGH_p, GH, BHF_p, HR, BRH_p, RS]],
[[A, E, B, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BR, BRF_p, QR, FQR_h, FQ, AFQ_p AF]],
↑、今回はこういうミスが多かった、ほとんど書かずに直したが。[A, E, B, G, H, R, Q, F]の時に、BRの間にSがある。それが抜けているという単純ミスだ。早く自動化してえ、できないんだっけか?
BR。B, S, R。BS, BSR_h, RS。
[[A, E, B, S, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FQ, AFQ_p AF]],
[[A, E, B, S, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FQ, AFQ_p AF]],
ES
[[A, E, S, R, Q, F], [EAF_p, AE, AEP_p, ES, ESR_p, RS, BRF_p, QR, FQR_h, FQ, AFQ_p AF]],
[[E, B, S], [BEP_p, BE, EBS_p, BS, BSE_p, ES]],
[[B, G, H, R], [GBS_p, BG, BGH_h, GH, BHF_p, HR, BRH_p, BR]]
同じくSが抜けている。ただしRBなので注意。
[[B, G, H, R, S], [GBS_p, BG, BGH_h, GH, BHF_p, HR, BRH_p, RS, BSR_h, BS]]
[[B, G, H, R, S], [GBS_p, BG, BGH_h, GH, BHF_p, HR, BRH_p, RS, BSR_h, BS]]
GS
[[B, G, S], [GBS_p, BG, BGE_p, GS, BSG_p, BS]]
[[G, H, R, S], [EGH_p, GH, BHF_p, HR, BRH_p, RS, GSR_p, GS]]
graph := [
A : [
[[F, D], [], []],
[[E, B], [], []]
]
,
B : [
[[E, A], [], []],
[[S, R, M], [], []],
[[G, H, C], [], []]
]
,
C : [
[[B, G, H], [], []],
[[D, M], [], []]
]
,
D : [
[[A, F], [], []],
[[M, C], [], []]
]
,
E : [
[[A], [], [B]],
[[P, S, G], [], []]
]
,
F : [
[[A], [], [D]],
[[Q, R, H], [], []]
]
,
G : [
[[B], [], [H, C]],
[[E, P, S], [], []]
]
,
H : [
[[B, G], [], [C]],
[[F, Q, R], [], []]
]
,
M : [
[[D], [], [C]],
[[B, S, R], [], []]
]
,
P : [
[[E], [], [S, G]],
[[Q], [], []]
]
,
Q : [
[[P], [], []],
[[F], [], [R, H]]
]
,
R : [
[[F, Q], [], [H]],
[[B, S], [], [M]]
]
,
S : [
[[E, P], [], [G]],
[[B], [], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△BES : [EBS, BE, BEP, ES, BSE, BS],
△BEG : [EBS, BE, BEP, EG, BGE, BG],
△BGS : [GBS, BG, BGE, GS, BSE, BS],
△BHR : [GBS, BH, BHF, HR, BRH, BR],
△BCM : [GBS, BC, BCD, CM, BMC, BM]
];
cluster_lst := [
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]],
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, G, S, P], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]],
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]],
[[B, G, S], [GBS_p, BG, BGE_p, GS, BSG_p, BS]],
[[G, H, C, M, R, S], [EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, GSR_p, GS]],
[[B, G, H, R, S], [GBS_p, BG, BGH_h, GH, BHF_p, RH, BRH_p, RS, BSR_h, BS]],
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[A, E, S, R, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, S], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]],
[[A, E, B, S, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]],
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR]]
[[A, E, P, S, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[S, G, H, C, M], [GSR_p, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS]],
[[A, E, P, S, G, H, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
[[H, C, M, D, F], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[E, B, S, P], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]],
[[M, D, F, Q, R], [BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRM_p, MR]],
[[A, E, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
[[E, B, G], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]],
[[B, G, H, R], [GBS_p, BG, BGH_h, GH, BHF_p, HR, BRH_p, BR]]
[[G, H, R, S], [EGH_p, GH, BHF_p, HR, BHR_p, RS, GSR_p, GS]],
[[R, M, D, F, Q], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_p, QR],
[[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP_p, FQ, AFQ_p, AF]],
[[P, S, G, H, R, Q], [QPS_p, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, PQR_p, PQ]],
[[A, E, P, S, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_h, FQ, AFQ_p, AF]],
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
AE + BE == AB;
AF + DF == AD;
BG + GH == BH;
BG + CG == BC;
BH + CH == BC;
GH + CH == CG;
DM + CM == CD;
EP + PS == ES;
EP + GP == EG;
FQ + QR == FR;
FQ + HQ == FH;
FR + HR == FH;
QR + HR == QH;
BR + MR == BM;
RS + MR == MS;
ES + GS == EG;
PS + GS == GP;
BS + RS == BR;
BS + MS == BM;
AEP_p + BEP_p == AEB_h;
AFQ_p + DFQ_p == AFD_h;
BGE_p + EGH_p == BGH_h;
BHF_p + CHF_p == BHC_h;
BMD_p + BMC_p == CMD_h;
EPQ_p + QPS_p == EPS_h;
FQP_p + PQR_p == FQR_h;
BRF_p + BRH_p == FRH_h;
FRM_p + HRM_p == FRH_h;
BRF_p + FRM_p == BRM_h;
BRH_p + HRM_p == BRM_h;
BSE_p + BSG_p == ESG_h;
ESR_p + GSR_p == ESG_h;
BSE_p + ESR_p == BSR_h;
BSG_p + GSR_p == BSR_h;
}いろいろ消えた。被ってたんで。
では続き。
[[P, S, G, H, R, Q], [QPS_p, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, PQR_p, PQ]],
RS
[[P, S, R, Q], [QPS_p, PS, ESR_p, RS, BRF_p, QR, PQR_p, PQ]],
[[S, G, H, R], [GSR_p, GS, EGH_p, GH, BHF_p, HR, BRH_p, RS]],
[[A, E, P, S, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_h, FQ, AFQ_p, AF]],
PQ
[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP, FQ, AFQ_p, AF]],
[P, S, R, Q], [QPS_p, PS, ESR_p, RS, BRF_p, QR, PQR_p, PQ]],
graph := [
A : [
[[F, D], [], []],
[[E, B], [], []]
]
,
B : [
[[E, A], [], []],
[[S, R, M], [], []],
[[G, H, C], [], []]
]
,
C : [
[[B, G, H], [], []],
[[D, M], [], []]
]
,
D : [
[[A, F], [], []],
[[M, C], [], []]
]
,
E : [
[[A], [], [B]],
[[P, S, G], [], []]
]
,
F : [
[[A], [], [D]],
[[Q, R, H], [], []]
]
,
G : [
[[B], [], [H, C]],
[[E, P, S], [], []]
]
,
H : [
[[B, G], [], [C]],
[[F, Q, R], [], []]
]
,
M : [
[[D], [], [C]],
[[B, S, R], [], []]
]
,
P : [
[[E], [], [S, G]],
[[Q], [], []]
]
,
Q : [
[[P], [], []],
[[F], [], [R, H]]
]
,
R : [
[[F, Q], [], [H]],
[[B, S], [], [M]]
]
,
S : [
[[E, P], [], [G]],
[[B], [], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△BES : [EBS, BE, BEP, ES, BSE, BS],
△BEG : [EBS, BE, BEP, EG, BGE, BG],
△BGS : [GBS, BG, BGE, GS, BSE, BS],
△BHR : [GBS, BH, BHF, HR, BRH, BR],
△BCM : [GBS, BC, BCD, CM, BMC, BM]
];
cluster_lst := [
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]],
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, G, S, P], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]],
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]],
[[B, G, S], [GBS_p, BG, BGE_p, GS, BSG_p, BS]],
[[G, H, C, M, R, S], [EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, GSR_p, GS]],
[[B, G, H, R, S], [GBS_p, BG, BGH_h, GH, BHF_p, RH, BRH_p, RS, BSR_h, BS]],
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[A, E, P, S, R, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, S, P], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]],
[[A, E, B, S, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]],
[[R, M, D, F, Q], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR]]
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
[[G, H, R, S], [EGH_p, GH, BHF_p, HR, BHR_p, RS, GSR_p, GS]],
[[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP_p, FQ, AFQ_p, AF]],
[[P, S, G, H, R, Q], [QPS_p, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, PQR_p, PQ]],
[[A, E, P, S, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_h, FQ, AFQ_p, AF]],
[[P, S, R, Q], [QPS_p, PS, ESR_p, RS, BRF_p, QR, PQR_p, PQ]],
[[S, G, H, R], [GSR_p, GS, EGH_p, GH, BHF_p, HR, BRH_p, RS]],
[[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP, FQ, AFQ_p, AF]],
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
AE + BE == AB;
AF + DF == AD;
BG + GH == BH;
BG + CG == BC;
BH + CH == BC;
GH + CH == CG;
DM + CM == CD;
EP + PS == ES;
EP + GP == EG;
FQ + QR == FR;
FQ + HQ == FH;
FR + HR == FH;
QR + HR == QH;
BR + MR == BM;
RS + MR == MS;
ES + GS == EG;
PS + GS == GP;
BS + RS == BR;
BS + MS == BM;
AEP_p + BEP_p == AEB_h;
AFQ_p + DFQ_p == AFD_h;
BGE_p + EGH_p == BGH_h;
BHF_p + CHF_p == BHC_h;
BMD_p + BMC_p == CMD_h;
EPQ_p + QPS_p == EPS_h;
FQP_p + PQR_p == FQR_h;
BRF_p + BRH_p == FRH_h;
FRM_p + HRM_p == FRH_h;
BRF_p + FRM_p == BRM_h;
BRH_p + HRM_p == BRM_h;
BSE_p + BSG_p == ESG_h;
ESR_p + GSR_p == ESG_h;
BSE_p + ESR_p == BSR_h;
BSG_p + GSR_p == BSR_h;
}目視で確認して、だいぶインチキというか削ったが、まあ単純ミスだろうし、良しとしよう。
って、角の和を登録するのを忘れていたか。
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
BM
とか、こういう段階で、クラスタのBかMの角がハーフで無くポジティブの時に、角の和を登録する。
今回はBがポジティブで、EBM(適当)とMBGが、足したらEBG_pになると登録する。
EBS_p + GBS_p == MBG_p、という具合。
他は無かった。いやあるんだが、まあそういうことだ。
graph := [
A : [
[[F, D], [], []],
[[E, B], [], []]
]
,
B : [
[[E, A], [], []],
[[S, R, M], [], []],
[[G, H, C], [], []]
]
,
C : [
[[B, G, H], [], []],
[[D, M], [], []]
]
,
D : [
[[A, F], [], []],
[[M, C], [], []]
]
,
E : [
[[A], [], [B]],
[[P, S, G], [], []]
]
,
F : [
[[A], [], [D]],
[[Q, R, H], [], []]
]
,
G : [
[[B], [], [H, C]],
[[E, P, S], [], []]
]
,
H : [
[[B, G], [], [C]],
[[F, Q, R], [], []]
]
,
M : [
[[D], [], [C]],
[[B, S, R], [], []]
]
,
P : [
[[E], [], [S, G]],
[[Q], [], []]
]
,
Q : [
[[P], [], []],
[[F], [], [R, H]]
]
,
R : [
[[F, Q], [], [H]],
[[B, S], [], [M]]
]
,
S : [
[[E, P], [], [G]],
[[B], [], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△BES : [EBS, BE, BEP, ES, BSE, BS],
△BEG : [EBS, BE, BEP, EG, BGE, BG],
△BGS : [GBS, BG, BGE, GS, BSE, BS],
△BHR : [GBS, BH, BHF, HR, BRH, BR],
△BCM : [GBS, BC, BCD, CM, BMC, BM]
];
cluster_lst := [
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]],
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, G, S, P], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]],
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]],
[[B, G, S], [GBS_p, BG, BGE_p, GS, BSG_p, BS]],
[[G, H, C, M, R, S], [EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, GSR_p, GS]],
[[B, G, H, R, S], [GBS_p, BG, BGH_h, GH, BHF_p, RH, BRH_p, RS, BSR_h, BS]],
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[A, E, P, S, R, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, S, P], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]],
[[A, E, B, S, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]],
[[R, M, D, F, Q], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR]]
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
[[G, H, R, S], [EGH_p, GH, BHF_p, HR, BHR_p, RS, GSR_p, GS]],
[[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP_p, FQ, AFQ_p, AF]],
[[P, S, G, H, R, Q], [QPS_p, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, PQR_p, PQ]],
[[A, E, P, S, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_h, FQ, AFQ_p, AF]],
[[P, S, R, Q], [QPS_p, PS, ESR_p, RS, BRF_p, QR, PQR_p, PQ]],
[[S, G, H, R], [GSR_p, GS, EGH_p, GH, BHF_p, HR, BRH_p, RS]],
[[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP, FQ, AFQ_p, AF]],
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
AE + BE == AB;
AF + DF == AD;
BG + GH == BH;
BG + CG == BC;
BH + CH == BC;
GH + CH == CG;
DM + CM == CD;
EP + PS == ES;
EP + GP == EG;
FQ + QR == FR;
FQ + HQ == FH;
FR + HR == FH;
QR + HR == QH;
BR + MR == BM;
RS + MR == MS;
ES + GS == EG;
PS + GS == GP;
BS + RS == BR;
BS + MS == BM;
AEP_p + BEP_p == AEB_h;
AFQ_p + DFQ_p == AFD_h;
BGE_p + EGH_p == BGH_h;
BHF_p + CHF_p == BHC_h;
BMD_p + BMC_p == CMD_h;
EPQ_p + QPS_p == EPS_h;
FQP_p + PQR_p == FQR_h;
BRF_p + BRH_p == FRH_h;
FRM_p + HRM_p == FRH_h;
BRF_p + FRM_p == BRM_h;
BRH_p + HRM_p == BRM_h;
BSE_p + BSG_p == ESG_h;
ESR_p + GSR_p == ESG_h;
BSE_p + ESR_p == BSR_h;
BSG_p + GSR_p == BSR_h;
EBS_p + GBS_p == MBG_p;
}これでセットアップは終わりだろう。長かった。
いや、誤解を生みそうだけど、今回のは終わりってことね。おそらくまだ続く。