09年度トライアル問題 問題10
『図で、AB = AE、DC = DEで、ABとDEは平行です。
また、角DAE = 53°、角AED = 106°、角CDE = 42°になっています。
このとき、角EBCの大きさを求めなさい。
(※図は正確ではありません。)
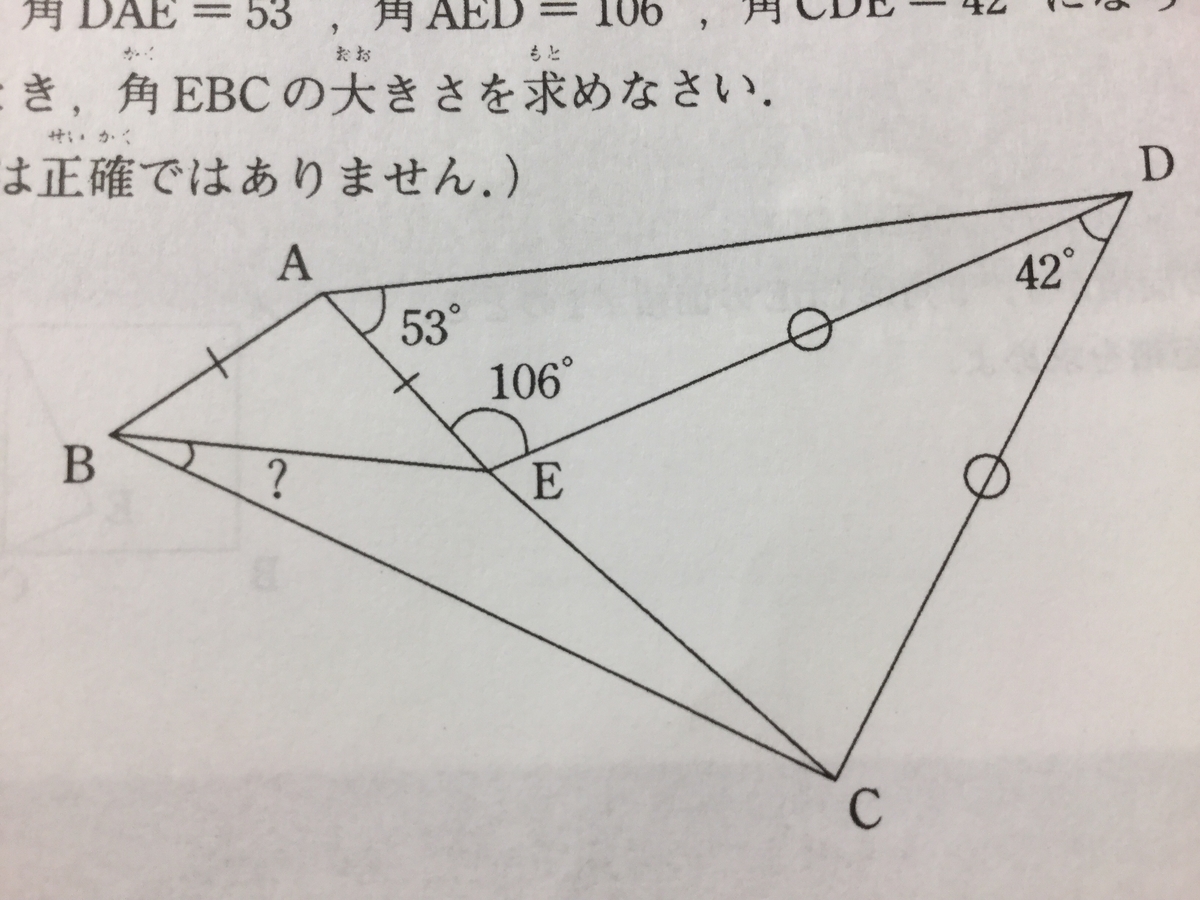 』
』
昨日の続きというか、角度のポジティブやネガティブを廃止して、時計回り順番で例えば角ABCと角CBAのように区別できないか、を挑戦するんだった。
しかし考えてみれば、anglewise_lst(時計回りリスト)における先とは何だろうか。先の方に存在すると言っても、一周回ってしまうのだから、後の方に存在するでもあるんじゃないか。
まあそう考えてみると、やはり180°という基準は必要ではあるのかもしれない、辺を基準に反対側の直線までという意味で。180°以上の角が存在する場合も、そういう角が2つできることは無いのだから、単に循環リストの前と後ろをくっつけるだけで良いだろう(いや厳密には循環リストですら無いのか、当初はともかく、今やその辺より前か後かで相対的に順番を記述しているのだから)。
人間がやるように、問題文を入力する際にポジティブやネガティブかを判別して入力できるというのも大きい。ただ、その記述を採用するならば、ますますangle_lstはいらないのではないか、という気もする。まあとにかく試してみなければ分からないだろう。
では初期条件。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B], [], [D, C]],
[D, [B, A], [], [C]],
[C, [A, D], [], [B]],
[B, [C], [], [A, D]]
]
];
coplanar_lst := [
[A, B, C, D, E]
];
triangle_lst := [
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
}
元々あったangle_lstのEと見比べてみよう。
angle_lst := [
E : [
[
[A, [], [], [D, C]],
[D, [A], [], [C]],
[C, [A, D], [], []]
]
,
[
[C, [], [], [B]],
[B, [C], [], []]
]
,
[
[B, [], [], [A, D]],
[A, [B], [], [D]],
[D, [B, A], [], []]
]
]
];
E : [
[A, [B], [], [D, C]],
[D, [B, A], [], [C]],
[C, [A, D], [], [B]],
[B, [C], [], [A, D]]
]
まあ細かい手順はともかく、工夫すれば置き換え可能そうな雰囲気が伝わってくる。この設定で進めてみよう。
休憩から明けてみて、やっぱり循環リストっていうのは並び方を変えても成立するものじゃないといけないわけで、clockwise_lstを前に戻すことは考えられないという気分だ。
始めてみて分かったけど、今日はイージーモードだな、ほとんど昨日のをコピペすれば良いわけだから。
では続き。
graphから辺の和や180°の角の和は無し。
parallel_lines_lst(とgraph)から、EAB == AED; #同じ大きさの対頂角・錯角の4角ずつが2セットあり得るわけだが、一方は貫く辺が先に来て、もう一方は貫かれる辺が先に来る。「キ」の字のような手元の図をどれだけ回しても、その関係は変わらない。まあよく考えてないが、多分大丈夫だろう
clockwise_lstから、
DAE + EAB == DAB、EAB + BAD == EAD、BAD + DAE == BAE、
みたいなのを延々と作っていく。まあ話が分かりやすくはなった。全部は書かない。
graphから、△ADE
△ABE
△BCE
△CDE
更にそれで登録した三角形から、ほぼそのままcluster_lstに登録
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]] #今回は点の並べ方が時計回りだけど、点の並べ方は反時計回りの方が、角とか辺が単純な見た目になる
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]] #例えばこのA, B, Eの順番は反時計回り。よく考えたらgraphを確認しなきゃいけないから、だからどうしたという話かもしれん
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]] #まあでもその場合も、graphでの一番最初に登録した同じ方向の点に置き換えれば良いだけだから、やっぱり簡単は簡単
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]] #作業は単純であるに越したことは無い。しかしプログラムだと考えない方が単純なんだよなあ
それらが全部終わってから、三角形定理ループを回す。しかし、どう明らかになるかはこの環境では分からない。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B], [], [D, C]],
[D, [B, A], [], [C]],
[C, [A, D], [], [B]],
[B, [C], [], [A, D]]
]
];
coplanar_lst := [
[A, B, C, D, E]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE]
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
}
作図
このままでは解答に至らないらしいので、作図に移る。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その26 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その25 - ニート歴10年からの数学日記、
セットアップ時の角の和の取得法について - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その21 - ニート歴10年からの数学日記の後半、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その18 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その17 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その16 - ニート歴10年からの数学日記、
辺りを参考にする、後ろに行くほどもう参考にならないと思うけど。
- 点と点を結ぶ
- 線を同じ分だけ延長する
- 二等辺三角形の作図1
- 二等辺三角形の作図2
- クラスタを貼り合わせる
- 正三角形の作図(必要だと分かった)
- ?正四角形の判定
- ?正五角形の判定
作業の流れはこんな感じだ。
「作図」
データ構造を上から見ていって
graphを更新する
平行線リストを更新する
clockwise_lstを更新する
平面上リストを更新する
「分析」
辺の和、直線の分割による角の和
平行線リストによって角のイコール
clockwise_lstによる角の和
三角形の発見
発見した三角形をそのままクラスタに
クラスタが割れているか
三角形定理ループ
「交点の発見」
Aから全ての辺で調べていく (一つの点における平均的な辺の数 ^3 * 点の数)
graphは簡単に更新できる
平行線リストを更新する
clockwise_lstに交点を追加する(交点の場合は他はいじる必要はない)
平面上リストにも交点を追加する
(交点が発生する辺を持つクラスタをどうするかは迷うな、次の分析のステップでやるかどうかが)
(以下、分析、交点の発見、分析、交点の発見、という風に続いていく)
では、点と点を結ぶ。今回もAとCを結ぶことにする。以下もほとんどコピペ。
graphのAとCにそれぞれ追加する。
次に、clockwise_lstの例えばAにおいて、CはDやEやBとどのような位置関係にあるか。
幸いそれぞれにおいて、AとCはそれぞれ繋がっている。だから位置関係も分かる。
(これは手元に図を描いて書いているのだが、いや今回は描いて無いのだが、)例えばDだと、時計回りでCからAからの順番なので、AにおいてCは、Dから時計回りで進んだ側にある。
Eだと、時計回りでAからCの順番なので、AにおいてCは、Eから時計回りで戻った側にある。
Bだと、時計回りでAからCの順番なので、AにおいてCは、Bから時計回りで戻った側にある。
つまり、
A : [
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]という風になるはずだ。
Cにおいてはそれぞれ逆なので、
C : [
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]という風になるはずだ。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[C], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[A], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B], [], [D, C]],
[D, [B, A], [], [C]],
[C, [A, D], [], [B]],
[B, [C], [], [A, D]]
]
];
coplanar_lst := [
[A, B, C, D, E]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE]
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
}
次に分析。またコピペする。
新しい辺の和や180°の角の和は無し。
clockwise_lstから新しい角を登録する。
次にgraphから三角形を探す。
結果、△ABC、△ACD、△ACEが見つかるはずだ。
そのままクラスタに登録する。
更に、クラスタの分割をチェックするが、分割されても三角形になるだけなので無視する。
三角形定理ループを回す。この環境では分からない。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[C], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[A], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B], [], [D, C]],
[D, [B, A], [], [C]],
[C, [A, D], [], [B]],
[B, [C], [], [A, D]]
]
];
coplanar_lst := [
[A, B, C, D, E]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE],
△ABC : [CAB, AB, ABC, BC, BCA, AC],
△ACD : [DAC, AC, ACD, CD, CDA, AD],
△ACE : [CAE, AC, ECA, CE, AEC, AE]
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]],
[[A, B, C], [CAB, AB, ABC, BC, BCA, AC]],
[[A, C, D], [DAC, AC, ACD, CD, CDA, AD]],
[[A, C, E], [CAE, AC, ECA, CE, AEC, AE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
}
三角関数で交点のチェックをする。計算量的に可能なうちは、全ての辺の組み合わせでチェックする。それが無理になってきたら、作図したり新しく明らかになったたびに、それだけチェックする。でもそうすると、グローバル変数だとかでデータ構造を扱う必要が出てくるのではないか、という気もする。キュー(リストを待ち行列のように使う)でタスクを管理すれば、そうでもないか。
以下ほぼコピペ。
そうすると、ACとDEの間に交点ができるのが分かるはず。それをFと名付ける。
交点なので、graphは簡単に更新できる。
平行線リストも更新する。
clockwise_lstにFを作る。
交点なので、他の点では手を加える必要は無い。また全ての角はポジティブなはずなので、どれを最初に持ってくるかは適当で良いだろう。
時計回りで「A, D, C, E」なのか「A, E, C, D」なのかは、交点を発見するのに使った三角を基準に考えれば良いだろう、多分。
180°ピッタリはどう登録しよう。両方に登録しようか。
平面上リストにも点Fを追加する。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[C, F], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[A, F], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E, F], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D, F], [], []]
]
,
F : [
[[A], [], [C]],
[[D], [], [E]]
]
];
parallel_lines_lst := [
[[A, B], [D, F, E]] #今回はDEの間で良かったけど、これも順番が分からないこともあるのかもな
];
clockwise_lst := [
A : [
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B], [], [D, C]],
[D, [B, A], [], [C]],
[C, [A, D], [], [B]],
[B, [C], [], [A, D]]
]
,
F : [
[A, [E, C], [], [D, C]],
[D, [A, E], [], [C, E]],
[C, [D, A], [], [E, A]],
[E, [C, D], [], [A, D]]
]
];
coplanar_lst := [
[A, B, C, D, E, F]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE],
△ABC : [CAB, AB, ABC, BC, BCA, AC],
△ACD : [DAC, AC, ACD, CD, CDA, AD],
△ACE : [CAE, AC, ECA, CE, AEC, AE]
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]],
[[A, B, C], [CAB, AB, ABC, BC, BCA, AC]],
[[A, C, D], [DAC, AC, ACD, CD, CDA, AD]],
[[A, C, E], [CAE, AC, ECA, CE, AEC, AE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
}
分析。またコピペ。
辺の和
AF + CF == AC; DF + EF == DE;
180°の角の和
AFC
CFA
DFE
EFD
()
clockwise_lstから角の和
三角形
△AFD
△AFE
△CFD
△CFE
そのままクラスタに
[[A, F, D], [DAC, AF, AFD, DF, EDA, AD]]
[[A, F, E], [CAE, AF, EFA, EF, AED, AE]]
[[C, F, D], [ACD, CF, DFC, DF, CDE, CD]]
[[C, F, E], [ECA, CF, CFE, EF, DEC, CE]]
クラスタ割れているか 辺ACと辺DEにFを加えて
AF, AFC, CF
DF, DFE, EF
なので
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]],
[[A, B, C], [CAB, AB, ABC, BC, BCA, AC]],
[[A, C, D], [DAC, AC, ACD, CD, CDA, AD]],
[[A, C, E], [CAE, AC, ECA, CE, AEC, AE]]
から
[[A, B, E, F, D], [DAB, AB, ABE, BE, BED, EF, EFD, DF, EDA, AD]],
[[A, D, F, E], [DAE, AD, EDA, DF, DFE, EF, AED, AE]],
[[C, D, F, E], [ECD, CD, CDE, DF, DFE, EF, DEC, CE]],
[[A, B, C, F], [CAB, AB, ABC, BC, BCA, CF, CFA, AF]],
[[A, C, D], [DAC, AF, AFC, CF, ACD, CD, CDA, AD]],
[[A, C, E], [CAE, AF, AFC, CF, ECA, CE, AEC, AE]]
三角形定理ループを回す。けどこの環境では無理。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[C, F], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[A, F], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E, F], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D, F], [], []]
]
,
F : [
[[A], [], [C]],
[[D], [], [E]]
]
];
parallel_lines_lst := [
[[A, B], [D, F, E]] #今回はDEの間で良かったけど、これも順番が分からないこともあるのかもな
];
clockwise_lst := [
A : [
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B], [], [D, C]],
[D, [B, A], [], [C]],
[C, [A, D], [], [B]],
[B, [C], [], [A, D]]
]
,
F : [
[A, [E, C], [], [D, C]],
[D, [A, E], [], [C, E]],
[C, [D, A], [], [E, A]],
[E, [C, D], [], [A, D]]
]
];
coplanar_lst := [
[A, B, C, D, E, F]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE],
△ABC : [CAB, AB, ABC, BC, BCA, AC],
△ACD : [DAC, AC, ACD, CD, CDA, AD],
△ACE : [CAE, AC, ECA, CE, AEC, AE]
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[A, F, D], [DAC, AF, AFD, DF, EDA, AD]],
[[A, F, E], [CAE, AF, EFA, EF, AED, AE]],
[[C, F, D], [ACD, CF, DFC, DF, CDE, CD]],
[[C, F, E], [ECA, CF, CFE, EF, DEC, CE]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]],
[[A, B, C], [CAB, AB, ABC, BC, BCA, AC]],
[[A, C, D], [DAC, AC, ACD, CD, CDA, AD]],
[[A, C, E], [CAE, AC, ECA, CE, AEC, AE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
AF + CF == AC;
DF + EF == DE;
}
新しい作図に入る。次は線の同じ長さ分だけの延長をやる。データの状態をリセットする。
昨日と同じように、辺CEをEの方向に延長する。先端にできる新しい点はFと名付ける。以下ほとんどコピペ。
まずgraphを更新する。CとEを更新して、また点Fを作る。
平行線リストの更新は無し。
次にclockwise_lstを更新する。Eを更新して、また点Fを作る。
Eにおいては、Cから180°なので、Cの両方にFを入れる。EにおけるF自体も、ちょうどそのように配置する。Eにおける他もそれに合わせる。
今回はおそらく偶然に上手く行った。
平面上リストにもFを追加する。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E, F], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], [F]],
[[D], [], []]
]
,
F : [
[[C, E], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B, F], [], [D, C]],
[D, [B, A, F], [], [C]],
[C, [A, D, F], [], [B, F]],
[B, [C], [], [A, D, F],
[F, [B, C], [], [A, D, C]]]
]
,
F : [
[C, [], [], []]
]
];
coplanar_lst := [
[A, B, C, D, E, F]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE]
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
CE == EF;
}
作図はしたので分析に入る。コピペ。
辺の和
CE + EF == CF;
180°の角
CEF、FEC
平行線リストによる角のイコールは、交点がまだ発生してないので無し
三角形は、探してないが、Eから伸ばしただけなのでどうせ無い。
だから新しくクラスタとして登録する三角形は無し
またクラスタの分割も、クラスタ内で新しく点と点が繋がるということは無いはずなので、無し
三角形定理ループを回す。しかしこの環境では結果は分からない
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E, F], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], [F]],
[[D], [], []]
]
,
F : [
[[C, E], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B, F], [], [D, C]],
[D, [B, A, F], [], [C]],
[C, [A, D, F], [], [B, F]],
[B, [C], [], [A, D, F],
[F, [B, C], [], [A, D, C]]]
]
,
F : [
[C, [], [], []]
]
];
coplanar_lst := [
[A, B, C, D, E, F]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE]
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
CE == EF;
CE + EF == CF;
}
交点の発見に入る。全部の辺の組み合わせを調べる。辺ABとの間にできることが分かるだろう。
ABとEFの交点Gを作図する。
まずgraphを更新する。
平行線リストも更新する。
clockwise_lstも更新する。実はG以外はイジる必要が無い。graphにおいて他は後から付け加えているだけなので。
発見時の三角を参考にすれば、登録できると思う、多分ね。
平面上リストも更新する。
で、前回と同じくクラスタも更新する。辺ABを含むものについて。
A, B → A, G, B
AB → AG, AGB, BG
あるいは
B, A → B, G, A
AB → BG, BGA, AG
(しかし後者は必要無かった)
もともとが
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
でこうなる
[[A, G, B, C, D], [DAB, AG, AGB, BG, ABC, BC, BCD, CD, CDA, AD]],
[[A, G, B, E, D], [DAB, AG, AGB, BG, ABE, BE, BED, DE, EDA, AD]],
[[A, G, B, E], [EAB, AG, AGB, BG, ABE, BE, BEA, AE]],
graph := [
A : [
[[B, G], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A, G], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E, F, G], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], [F, G]],
[[D], [], []]
]
,
F : [
[[C, E, G], [], []]
]
,
G : [
[[A], [], [B]],
[[F], [], [E, C]]
]
];
parallel_lines_lst := [
[[A, G, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B, F], [], [D, C]],
[D, [B, A, F], [], [C]],
[C, [A, D, F], [], [B, F]],
[B, [C], [], [A, D, F],
[F, [B, C], [], [A, D, C]]]
]
,
F : [
[C, [], [], []]
]
,
G : [
[F, [B, E], [], [A, E]],
[A, [F, B], [], [E, B]],
[E, [A, F], [], [B, F]],
[B, [E, A], [], [F, A]]
]
];
coplanar_lst := [
[A, B, C, D, E, F, G]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE]
];
cluster_lst := [
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]],
[[A, G, B, C, D], [DAB, AG, AGB, BG, ABC, BC, BCD, CD, CDA, AD]],
[[A, G, B, E, D], [DAB, AG, AGB, BG, ABE, BE, BED, DE, EDA, AD]],
[[A, G, B, E], [EAB, AG, AGB, BG, ABE, BE, BEA, AE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
CE == EF;
CE + EF == CF;
}
分析する。以下もコピペ。
辺の和
CE + EG == CG;
AG + BG == AB;
FG + EG == EF;
FG + CG == CF;
180°の角
CEG
GEC
AGB
BGA
EGF
FGE
平行線リストによって角のイコール。ぶっちゃけ手順は忘れた
GED == EGB;
GED == FGA;
DEC == AGE;
DEC == BGF;
clockwise_lstによる角の和。面倒なので勝手に登録してくれてると見なす。手順は単純だろうし。
三角形の発見
△AEG
△BCG
△BEG
発見した三角形をそのままクラスタに
[[A, E, G], [EAB, AE, FEA, EG, AGE, AG]]
[[B, C, G], [ABC, BC, BCE, CG, EGB, BG]]
[[B, E, G], [ABE, BE, BEF, EG, EGB, BG]]
クラスタが割れているか 今回はGだけを確認すれば良いみたいだ
[A, G, B, C, D]
CG
[A, G, C, D]
[G, B, C]
[[A, G, C, D], [DAB, AG, AGE, CG, ECD, CD, CDA, AD]]
[A, G, B, E, D]
EG
[A, G, E, D]
[G, B, E]
[[A, G, E, D], [DAB, AG, AGE, EG, FED, DE, EDA, AD]]
三角形定理ループを回す。この環境だと無理だが
graph := [
A : [
[[B, G], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A, G], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E, F, G], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], [F, G]],
[[D], [], []]
]
,
F : [
[[C, E, G], [], []]
]
,
G : [
[[A], [], [B]],
[[F], [], [E, C]]
]
];
parallel_lines_lst := [
[[A, G, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B, F], [], [D, C]],
[D, [B, A, F], [], [C]],
[C, [A, D, F], [], [B, F]],
[B, [C], [], [A, D, F],
[F, [B, C], [], [A, D, C]]]
]
,
F : [
[C, [], [], []]
]
,
G : [
[F, [B, E], [], [A, E]],
[A, [F, B], [], [E, B]],
[E, [A, F], [], [B, F]],
[B, [E, A], [], [F, A]]
]
];
coplanar_lst := [
[A, B, C, D, E, F, G]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE],
△AEG : [EAB, AE, FEA, EG, AGE, AG],
△BCG : [ABC, BC, BCE, CG, EGB, BG],
△BEG : [ABE, BE, BEF, EG, EGB, BG]
];
cluster_lst := [
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]],
[[A, G, B, C, D], [DAB, AG, AGB, BG, ABC, BC, BCD, CD, CDA, AD]],
[[A, G, B, E, D], [DAB, AG, AGB, BG, ABE, BE, BED, DE, EDA, AD]],
[[A, G, B, E], [EAB, AG, AGB, BG, ABE, BE, BEA, AE]],
[[A, E, G], [EAB, AE, FEA, EG, AGE, AG]],
[[B, C, G], [ABC, BC, BCE, CG, EGB, BG]],
[[B, E, G], [ABE, BE, BEF, EG, EGB, BG]],
[[A, G, C, D], [DAB, AG, AGE, CG, ECD, CD, CDA, AD]],
[[A, G, E, D], [DAB, AG, AGE, EG, FED, DE, EDA, AD]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
CE == EF;
CE + EF == CF;
CE + EG == CG;
AG + BG == AB;
FG + EG == EF;
FG + CG == CF;
GED == EGB;
GED == FGA;
DEC == AGE;
DEC == BGF;
}
次の作図に行く。前回においては二等辺三角形の作図を飛ばして、クラスタの作図に行っているので、今回もそうする。コピペする。
△ADEのクラスタを、DEで回転させるように貼り付ける。新しい点をFとする。
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
から
[[F, D, E], [EFD, DF, FDE, DE, DEF, EF]],
みたいなのを複製したい。
つまり今回は、角における位置がそれぞれ入れ替わるわけだ。
他は良いんだけど、angle_lstが難しい。
新しく作るFはAにおけるDとEの順番を反転させるだけで良い。しかしDとEは、例えばDの角において、Eを基準にAが時計回りで先側にあるなら、反転させたら戻った側にあるとは言えるが、それ以上言えるだろうか。
人間は、見た目や実際の角度を参考にして判断するわけだが。
反対側に辺を延長する作図ほどは単純じゃなくて、やっぱり大きさの比較が必要になる。
今まではclockwise_lstの点に属する辺の一つ一つは、「[[時計回り反時計回りのどちらか], [隣り合う可能性がある], [時計回り反時計回りのどちらか]]」というつもりだった。
しかし、「[[時計回り反時計回りのどちらか], [両方のどちらか分からない], [時計回り反時計回りのどちらか]]」にすべきかと考えている。
あるいは、「[[時計回り反時計回りのどちらか], [隣り合う可能性がある], [時計回り反時計回りのどちらか], [両方のどちらか分からない]]」でも良いかもしれない。
大は小を兼ねるというか、そうすると、人間が初期条件でポジティブかネガティブか判断できないという想定でも、全てをどちらか分からないに入れず、現に隣り合っているものを隣り合う可能性があるに入れることで、やりやすくなるはず。両方に隣り合う可能性があるものがあれば、そこにあるのだろうという感じで。新しく辺を付ける時は可能性が追加される感じで、消せる可能性はどんどん消していく。
右隣に隣り合う可能性があるとか、左隣に隣り合う可能性があるとか、そういう風に細かく分けても良いけど、どうしようかな。
「[[反時計回りに180°以内], [隣り合う可能性がある], [時計回りに180°以内], [両方のどちらか分からない]]」というのが現在の第一候補ではある。
「[[反時計回りに180°以内], [反時計回りで隣り合う可能性がある], [時計回りで隣り合う可能性がある], [時計回りに180°以内], [両方のどちらか分からない]]」という風にするかどうかで迷っている。明らかにクドいんだよなあ。反時計回りと時計回りで使い分けることがあるか、ってことなんだけど。
まあ別に、そうした所で2回登録する必要があるだけで、思考に混乱があるわけじゃないから、念の為にそちらを採用してみようか。次回からはそうしよう。
ああいや、時計回り反時計回りのどちらか、からの変更も考えなければいけないのか。いやとにかく迷った二つのうちの後者を試して、様子を見て前者に切り替えて、その時にそこをきっちりするかを考えれば良い。
いや、どうしようかなあ。例えば反時計回りで隣り合っている場合は、「[..., 隣り合う一方], [..., 隣り合う一方], [...], [...], [...]」という感じになるんだろうか。
隣り合う可能性があると、どちらかの方向に180°以内にあるは、違う概念なんじゃないか。どうせ180°以内とか、どちらか分からないとか、記述するのだから、迷った内の後者は意味が無いのではないか。
それならば、「[[反時計回りに180°以内], [隣り合う可能性がある], [時計回りに180°以内], [両方のどちらか分からない]]」かな。
反時計回り、時計回りでハッキリさせるのかも考える必要があるし。
寝不足なせいか分からない。どれが良いかいつかは定まると思うけど。
「[[時計回り反時計回りのどちらか], [両方のどちらか分からない], [時計回り反時計回りのどちらか]]」が基本として、時計回り反時計回りでハッキリさせるか、隣り合う可能性があるという項を入れるか、の二つを考える必要があるということだろうが。
とりあえずその基本で行くと、今回はこうなるだろう。
D : [
[F, [], [C, E, A], []],
[C, [], [F], [E, A]],
[E, [C, F], [], [A]],
[A, [C, E], [F], []]
]
,
E : [
[F, [], [A, D, C, B], []],
[A, [B], [F], [D, C]],
[D, [B, A], [], [C, F]],
[C, [A, D], [F], [B]],
[B, [C], [F], [A, D]]
]
まずDにおいて、Eから見たAの反対側にFがあるはずだ。Eにおいても、Dから見たAの反対側にFがあるはずだ。
Dにおいて、Aから見たEの反対側にFがあるとは、当たり前だが言えないだろう。間違えたけど、実際に同じ方向にある。
(Fから見たEは?)
まあEを中心としたAとFの角は、角度が212と168なんで、そこら辺から判断が付くんじゃないかと思うが。AEFとかFEAで180°以上か以下かを調べれば良い。
風邪気味らしくて、寝て起きて今書いているけど、いろいろと駄目だな。
見た目的には時計回りで隣り合っていても、角度が分からないなら反時計回り側の180°にあるかもしれないわけで、[隣り合う可能性がある]とその180°だけで、[時計回り側で隣り合う可能性がある]を表現することはできない。
その上で、角度を調べるということなら、あの基本形に加えて、時計回りか反時計回りかをハッキリさせて、その上でFEAが180°以下だったら、Fの右辺の時計回り側にAを挿入して、Aの左辺の反時計回り側にFを挿入する、という風にすれば良いだろう。AEFは360 - FEAで登録してあるので、調べなくても良い。その作業を、不確定なものごとにやっていけば良い。
EにおいてはDの条件からもう少し絞れるだろう。
まあ、今日はここまでで良いかな。形式も変わることだし。次回どうするかは明日決める。