12年度ファイナル問題 問題7
『図で、AD=AC、BD=DCです。いま、AD上にPD+FD=BFとなるような点Pをとります。角FAE=24度、角BFD=35度であるとき、角PCDの大きさを求め、考え方も書きなさい。
※ただし、図は正確とは限りません。
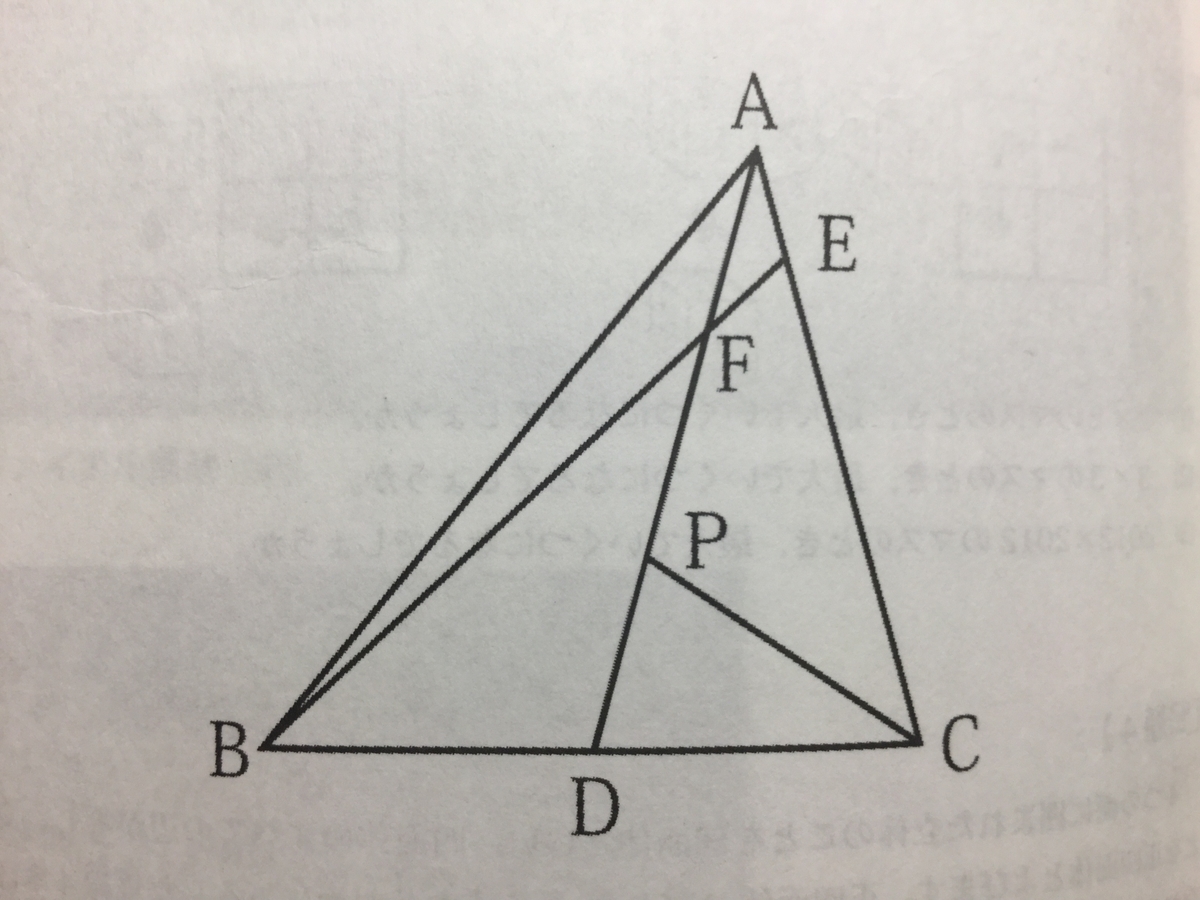 』
』
今回で普通の問題は一段落つけるつもりでいる。今の予定ではだが。
今はプログラムでいう仕様を決めている段階なわけで、一通りの種類の問題をチェックし終わった時に、自動化できるか模索しようと思う。
全体の流れとしては、まず初期条件を設定して、分析して、それからは以下の流れに従う。
「作図」
データ構造を上から見ていって
graphを更新する
平行線リストを更新する
clockwise_lstを更新する
平面上リストを更新する
「分析」
直線の分割による辺の和、角の和
平行線リストによって角のイコール
clockwise_lstによる角の和
三角形の発見
発見した三角形をそのままクラスタに
クラスタが割れているか
三角形定理ループ
「交点の発見」
Aから全ての辺で調べていく (一つの点における平均的な辺の数 ^3 * 点の数)
graphは簡単に更新できる
平行線リストを更新する
clockwise_lstに交点を追加する(交点の場合は他はいじる必要はない)
平面上リストにも交点を追加する
(交点が発生する辺を持つクラスタをどうするかは迷うな、次の分析のステップでやるかどうかが)
(以下、分析、交点の発見、分析、交点の発見、という風に続いていく)
具体的な作図の種類はこんな感じだ。
- 点と点を結ぶ
- 線を同じ分だけ延長する
- 二等辺三角形の作図1
- 二等辺三角形の作図2
- クラスタを貼り合わせる
- 正三角形の作図(必要だと分かった)
- ?正四角形の判定
- ?正五角形の判定
では初期条件。
graph := [
A : [
[[B], [], []],
[[F, P, D], [], []],
[[E, C], [], []]
]
,
B : [
[[A], [], []],
[[F, E], [], []],
[[D, C], [], []]
]
,
C : [
[[A, E], [], []],
[[P], [], []],
[[B, D], [], []]
]
,
D : [
[[B], [], [C]],
[[A, F, P], [], []]
]
,
E : [
[[A], [], [C]],
[[B, F], [], []]
]
,
F : [
[[A], [], [P, D]],
[[B], [], [E]]
]
,
P : [
[[A, F], [], [D]],
[[C], [], []]
]
];
parallel_lines_lst := [
];
clockwise_lst := [ #[その辺の記号のgraphの一番最初, 反時計回り側180°, どちらか不明, 時計回り側]
A : [
[E, [], [], [F, B]],
[F, [E], [], [B]],
[B, [E, F], [], []]
]
,
B : [
[A, [], [], [F, D]],
[F, [A], [], [D]],
[D, [A, F], [], []]
]
,
C : [
[B, [], [], [P, A]],
[P, [B], [], [A]],
[A, [B, P], [], []]
]
,
D : [
[B, [C], [], [A, C]],
[A, [B], [], [C]],
[C, [B, A], [], [B]]
]
,
E : [
[C, [A], [], [B, A]],
[B, [C], [], [A]],
[A, [C, B], [], [C]]
]
,
F : [
[B, [E, P], [], [E, A]],
[A, [P, B], [], [P, E]],
[E, [B, A], [], [B, P]],
[P, [A, E], [], [A, B]]
]
,
P : [
[A, [D], [], [D, C]],
[C, [A], [], [D]],
[D, [A, C], [], [A]]
]
];
coplanar_lst := [
[A, B, C, D, E, F, P]
];
triangle_lst := [
];
cluster_lst := [
];
always {
AD == AC;
BD == CD;
DP + DF == BF;
EAF == 24;
PFB == 35;
}
分析に移る。
#単純な辺の和をgraphから生成
#単純な角の和をclockwise_lstから生成
180 == #graphから生成
180 < #clockwise_lstから生成
180 > #clockwise_lstから生成できる
もうこういうのは飛ばしちゃおう、これだけ書いて。
平行線リストは無し。
三角形の発見、
発見した三角形をそのままクラスタに、
クラスタが割れているか、
も飛ばしちゃおう。
で三角形定理ループ。
分析自体は、もうやろうと思えば自動化できる。交点の発見も、発見するだけならおそらく自動化できると思う。論点は一つ一つの作図だろう。
では作図に移る。作図は、
graphを更新する
平行線リストを更新する
clockwise_lstを更新する
平面上リストを更新する
というステップを踏むんだった。
じゃあ、BとPを結んでみよう。
graphの更新は当たり前にできるだろう。平行線リストも平面上リストも特に変更は無い。
問題はclockwise_lstの更新だ。考えるために、元々のclockwise_lstから引用する。
B : [
[A, [], [], [F, D]],
[F, [A], [], [D]],
[D, [A, F], [], []]
]
P : [
[A, [D], [], [D, C]],
[C, [A], [], [D]],
[D, [A, C], [], [A]]
]本当はE以外の全ての点を共有しているのだが。
これは、例えばAとCで同じ時計回り同士だと、AとCのどちらが内側かが分からない。位置を入れ替えることができるんで、どの角の間にあるのかの参考にならない。
まあ180°以下かどうか確かめる必要はあるが、FBDがポジティブな所から、しっかりFとD(P側だとDとA)の間だと分かるだろう。
で分析して、更には交点を探したり何だりする。
次は辺の延長。交点は後から探すしどこでも良いのだけど、ADと同じだけAから延ばしてみようか。
graphを更新して、平面上リストに新しい点を追加して、平行線リストは特に何も無くて。
これも問題は、clockwise_lstだろう。考えるために引用する。
A : [
[E, [], [], [F, B]],
[F, [E], [], [B]],
[B, [E, F], [], []]
]新しい点をGとすると、Fの左と右をひっくり返したような、「[G, [B, F], [], [E, F]]」という風になるのだと思う。
で性質上、EやBにおいてはFの反対側に来る。つまりこうなる。
A : [
[E, [G], [], [F, B]],
[F, [E, G], [], [B, G]],
[B, [E, F], [], [G]],
[G, [B, F], [], [E, F]]
]これで分析して、交点を探せば良いだろう。
次は二等辺三角形の作図。2つの角を比較して、大きい側と小さい側で2種類の作図がある。
三角形AEFをモデルにしよう。角Aは24°だし、角Fは角BFDの対頂角なので、35°だ。
△AEF : [EAF, AE, FEA, EF, EFA, AF]
EAF == 24
EFA == 35
じゃあ2つの角を比較して、EAF < EFAが明らかになったとする。
まず小さい方の角の作図から検討する。小さい方の角と頂点の間に、底辺のもう一方の端点から辺を引いて、二等辺三角形を作図する。
つまり、辺AEの間に、点Fから辺を引く。新しい点はGとする。
graph := [
A : [
[[B], [], []],
[[F, P, D], [], []],
[[E, C, G], [], []]
]
,
E : [
[[A, G], [], [C]],
[[B, F], [], []]
]
,
F : [
[[A], [], [P, D]],
[[B], [], [E]],
[[G], [], []]
]
,
G : [
[[A], [], [E, C]],
[[F], [], []]
]まあ、このCは、つまりgraphにおける辺の上の点の順番は、調べれば分かるだろう。
平行線リストも平面上リストも、そんなに複雑では無い。
問題は、やはりclockwise_lstだろう。
三角形としては時計回りで、A, E, F, A, E, Fというような順番になっているわけだが。
clockwise_lst := [ #[その辺の記号のgraphの一番最初, 反時計回り側180°, どちらか不明, 時計回り側]
F : [
[G, [A], [B, P], [E]],
[B, [E, P], [G], [E, A]],
[A, [P, B], [], [P, E, G]],
[E, [B, A, G], [], [B, P]],
[P, [A, E], [G], [A, B]]
]
,
G : [
[E, [A], [], [F, A]],
[F, [E], [], [A]],
[A, [E, F], [], [E]]
]Gにおいては、AとEの時計回りで先側から、E, F, Aの順番になる。
Fにおいては、Aからは時計回り側、Eからは反時計回り側にGがあるのは確定。
で本当は、BやPにおいても、ちょっと見にくいがそれぞれEやAをひっくり返しただけなので、確定するはずなのだが。
ちょっと脱線するが、clockwise_lstにおける、不確定な点の位置の絞り込みについて考えてみたい。
結果的に、最初はどれでも良いが例えばB, A, G, E, Pの順番なので、下のような順番になってほしい。とりあえず並び替えただけだが。
clockwise_lst := [ #[その辺の記号のgraphの一番最初, 反時計回り側180°, どちらか不明, 時計回り側]
F : [
[B, [E, P], [G], [E, A]],
[A, [P, B], [], [P, E, G]],
[G, [A], [B, P], [E]],
[E, [B, A, G], [], [B, P]],
[P, [A, E], [G], [A, B]]
]思考回路としては、一番制約が強いEとAの、とりあえずAに着目して、それからEとの整合性を取る感じなのかな?
F : [
[B, [E, P], [G], [E, A]],
[A, [P, B], [], [P, E, G]],
[G, [A], [B, P], [E]]
[E, [B, A, G], [], [B, P]],
[P, [A, E], [G], [A, B]],
]循環リストで、Aから後ろ2つにPとBがあって、Aから前3つにPとEとGがある、というような制約なのだけど。
位置の制約と呼んでいたっけか。記述法はもう忘れたけど。
とにかく、そういう制約と、後は例えばBFGが180°以上か以下か。180°以上だったらBにおいてはGを右に振り分けて、以下だったら左に振り分ける。
角度が明らかになって、その方法で制約がハッキリすることもあるだろうから、この絞り込みのセクションは作図とは別に設けたほうが良いだろう。
もう一方の二等辺三角形の作図も、似たようなものになるだろう。次の作図に行く。
クラスタの貼り合わせをする。じゃあその、三角形AEFをクラスタと捉えることにしよう。
[[A, E, F], [EAF, AE, FEA, EF, EFA, AF]]
例えばAEで、三角形AEFとそのコピー、三角形AEGを貼り合わせるとする。
同じ長さの辺で、4種類の貼り付け方がある。今回はコピーなので、3種類だろうが。
同じ方向の2種類は、角度や辺の大きさの対応で分ければ良いのかな。同じ側は[A, E, G]で、反対側は[E, A, G]になるだろう。
クラスタからグラフを生成することは簡単だろうし、平行線リストも平面上リストも、まあそこまでは難しくないだろう。やはり問題はclockwise_lstだ。
まあ反対側に作る場合は、こんな感じじゃないだろうか。
clockwise_lst := [
A : [
[G, [], [B, F], [E]],
[E, [G], [], [F, B]],
[F, [E], [G], [B]],
[B, [E, F], [G], []]
]
,
E : [
[G, [A], [C, B], []],
[C, [A], [G], [B, A]],
[B, [C], [G], [A]],
[A, [C, B], [], [C, G]]
]
];AにおけるEでは、Fの反対側にあるのは確定。他はBはもちろん、Fですら180°のどちらかは分からないんじゃないか。後から角度とかで絞り込めば良い。
Eにおいても、似たような感じだろう。
次は同じ側に作る場合。
clockwise_lst := [
A : [
[G, [E], [F, B], []],
[E, [], [], [F, B, G]],
[F, [E], [G], [B]],
[B, [E, F], [G], []]
]
,
E : [
[G, [], [C, B], [A]],
[C, [A], [G], [B, A]],
[B, [C], [G], [A]],
[A, [C, B, G], [], [C]]
]
];今度は逆に、AにおけるEとかで同じ側にあるのが確定って感じじゃないか。他はBとかはもちろん、Fも分からないんじゃないか、どちらの角が大きいかっていうのは。
こんな感じで良いだろう。次回は算数オリンピックの同じような問題から変な問題を見つけるか、ジュニア算数オリンピックの面積の問題をやるか、じゃないか。