sasaharayuugo.net

94年度ファイナル問題　問題4

『図1のような、AとBの二つの三角形があります。それぞれを、図2のように切り分けると、Aからできる二つの三角形と、Bからできる二つの三角形とで、たがいに相似（そうじ）の三角形の組が二組となります。

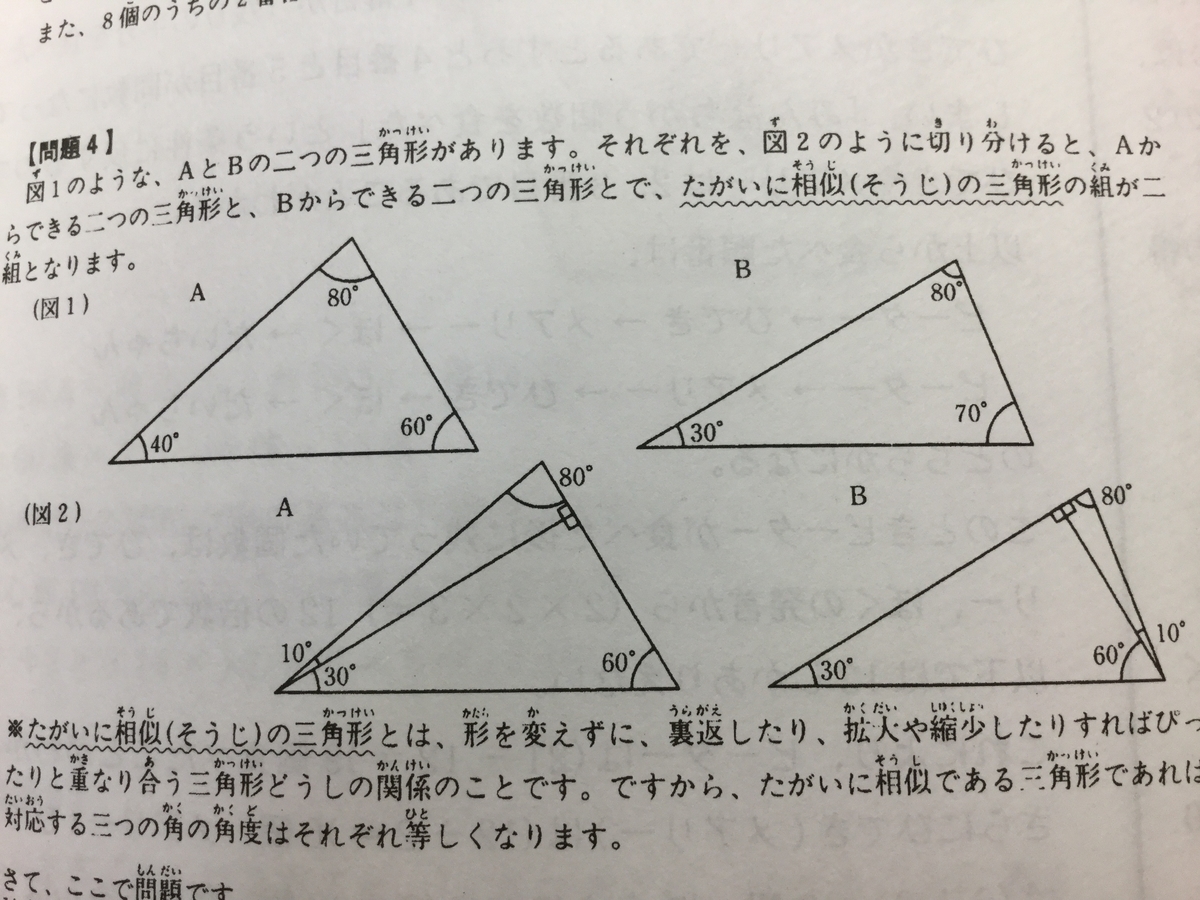
※たがいに相似（そうじ）の三角形とは、形を変えずに、裏返したり、拡大や縮小したりすればぴったりと重なり合う三角形どうしの関係のことです。ですから、たがいに相似である三角形であれば、対応する三つの角の角度はそれぞれ等しくなります。

さて、ここで問題です。
今度は、直角二等辺三角形と正三角形とをそれぞれ三つの三角形に切り分けます。
直角二等辺三角形からできる三つの三角形と、正三角形からできる三つの三角形とで、たがいに相似の三角形の組が三組となるように、切れこみを入れなさい。
また、切り分けてできる三角形のすべての角に、角度を書き入れなさい。』

今までの問題は、角度や辺の値を明らかにせよというものだったが、これは作図がゴールになっている。今までの自分の体系で言えば、クラスタの作図がゴールになっている。
それも、クラスタを分割したら、分割元のクラスタは答えから外さなければいけない。

決められた、それも値を求める問題に無い種類の作図をステップとして定義して、答えに至る。
cluster_lstのリストの数字を登録するリストを定義して、その中の一つをcluster_lstから選び、分割して、その数字自体は消す。

既存の流れから、他の作図を外し、その作図に差し替える。リストの登録もその作図のステップの内に入れて良いだろう。
作図をする際には角度は具体的には決めない方が良いだろう。三角形1つであれば3通りの作図、2つであれば6通りの作図、3つであれば9通りの作図がある。その結果同士で、リストに登録されたクラスタの、角度の集合を用意し、2つの結果のその集合がイコールだという制約を入れて、結果が一つでも出れば打ち止めにする（結果の一つ、という風に命令して、最適化は言語側がやってくれるだろう）。

応用だが、そこまで難しい応用というわけじゃない。こういう問題の数が出揃い次第、自然言語でない記述方法を考えたいと思う。
　

98年度ファイナル問題　問題6

『ある1つの多角形を何本かの直線で切りはなし、いくつかの多角形に分けました。
すると、分けてできた多角形の辺の数の合計は、もとの多角形の辺の数より13本多く、内角の合計はもとの多角形の内角の和の1.3倍になりました。
もとの多角形は何角形でしたか。また、それをいくつに分けましたか。』

答えを見ると、切り離すたびにバラバラのクラスタとして解釈するらしくて、そうすると辺の数の増え方は、頂点同士を結んで2本、頂点と辺を結んで3本、辺同士を結んで4本増える。
そこから、3回しか分割しない場合は12にしかならず足りないし、7回も分割すると14になり超えてしまう。よって分割回数は4回から6回。

4回の場合は、2本3本4本4本、3本3本3本4本。
5回の場合は、2本2本2本3本4本、2本2本3本3本3本。
6回の場合は、2本2本2本2本2本3本。

頂点同士を結んだ時には内角は増えない。頂点と辺を結んだときには180°増える。辺同士を結んだ時には360°増える。
4回の場合は、どちらにせよ180°×5増えてしまう。6回の場合は180°×1しか増えない。どちらにせよ元々の1.3倍にはならない。
5回の場合は、180°×3増える。それで1.3倍になったわけだから、元々の内角は180°×10。よって12角形だったと分かるらしい。

ステップごとの増加分にだけ着目して、制約で解くということだけど、どう考えれば良いのかな。
いや、もっと原始的な記述でも解けるけど、計算量を減らそうと工夫するとこうなるという話か？「いくつかの多角形」の部分も、マックスを決めればできないことも無いんだが。
こういう問題から、最終的には代数学や解析学なんだろうなあと思うんだよね。代数学とかの群論とか基礎の部分は、コンピューターのメタファーや手元での演算でもう少し簡単になるはずだと思うが。
　

12年度トライアル問題　問題10

『長方形ABCDの辺BC上にAD=AEとなるようにEを取ります。
いま、AD=12cm、ED=4cmです。このとき、BEの長さを求めなさい。

』

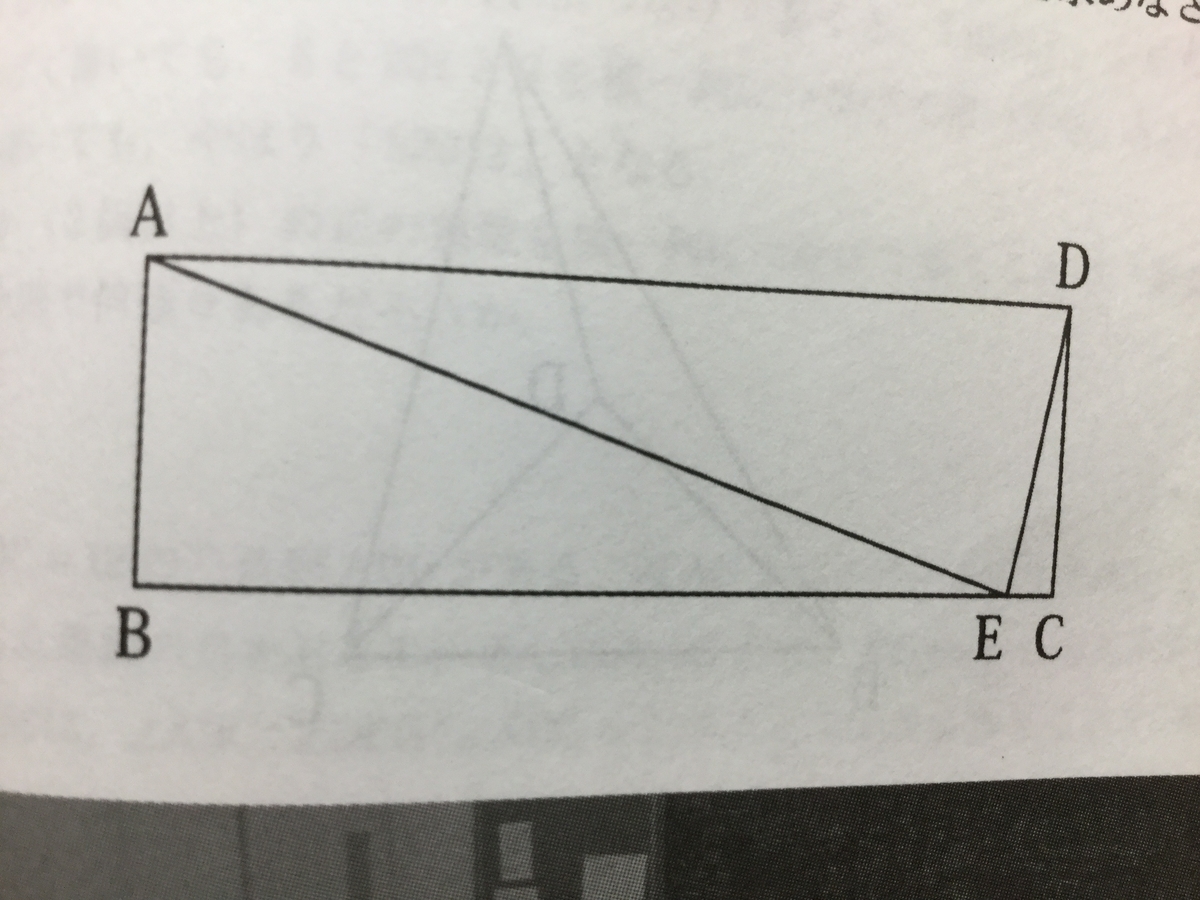これは一見既存の種類の問題だが、三角形ADEの角Aから垂線を下ろすという、新しい作図が必要になる。
これが二等辺三角形に限定して良いのか、それとも全ての三角形でこの作図が必要になるのか、今は分からないが、とりあえず前者だと解釈する。
まあ作図の種類を増やせば良いだけなのだが。角度が違うだけなので、方法論としても難しくは無い。
　

13年度トライアル問題　問題10

『図の四角形ABCDで、点E、F、G、H、MはAE : EB = AF : FD = 2 : 5、BG : GH : HC = 3 : 2 : 2、CM = DMを満たす辺上の点です。いま、EG、FH上にそれぞれEP = PG、FQ = QHとなる点P、Qをとるとき、PQ : BMを求めなさい。

』

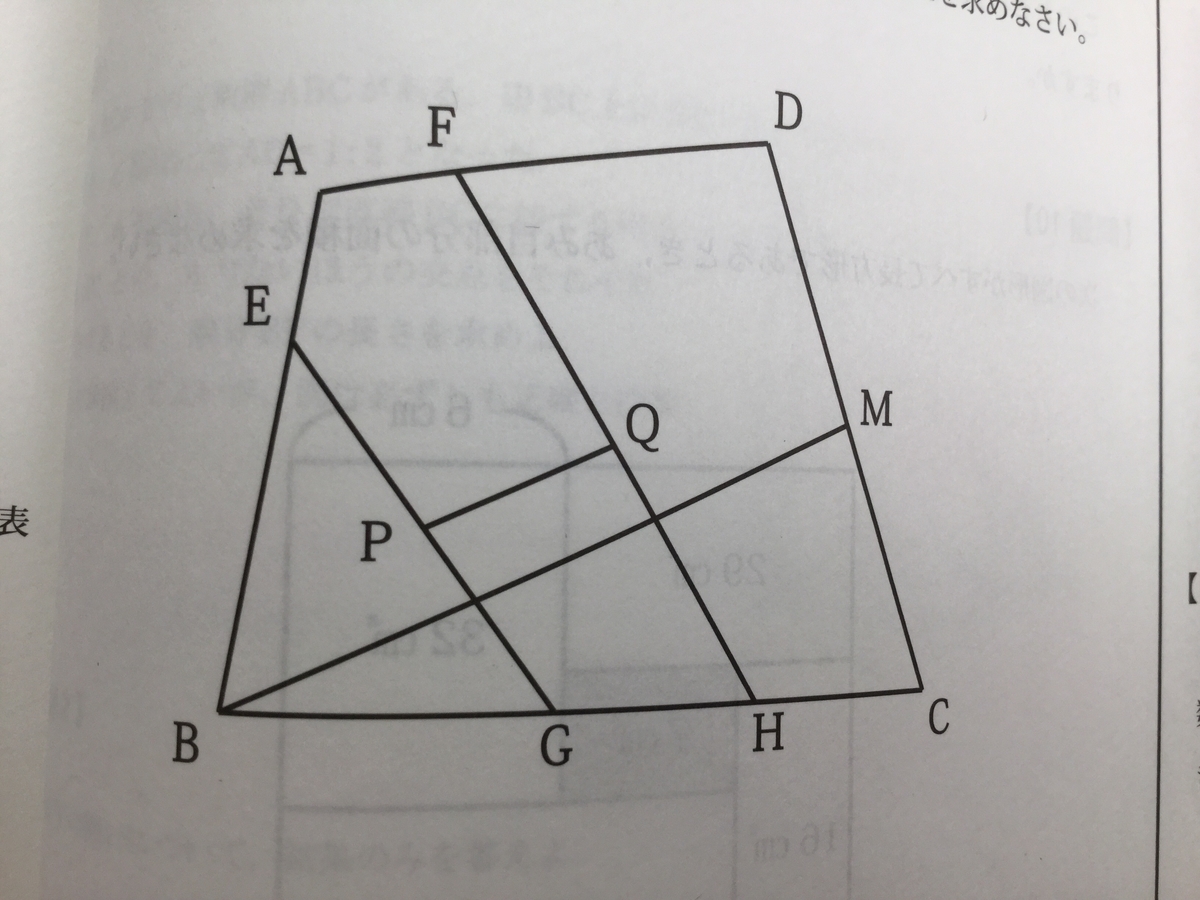相似の概念が必要になる。
辺CDに、2:5の点を打って、点F、E、Hとその点を結ぶことで、平行四辺形ができるらしい。
最初は答えを読んでもなぜそうなるのかが分からなかったのだが、対角線を基準に相似で5\7になったり、2\7になったりで、辺の長さが向かい合わせでイコールになるので平行四辺形になるということらしい。

ということで、これからは、二等辺三角形の頂点から垂線を落とす作図に加えて、相似の概念も導入する。
角度が全て同じだったり、全ての辺の比率が同じだったり、同じ角度の角を比率が同じ辺が挟んでいたりしたら、その二つの三角形は相似ということになる。