sasaharayuugo.net

94年度トライアル問題　問題7

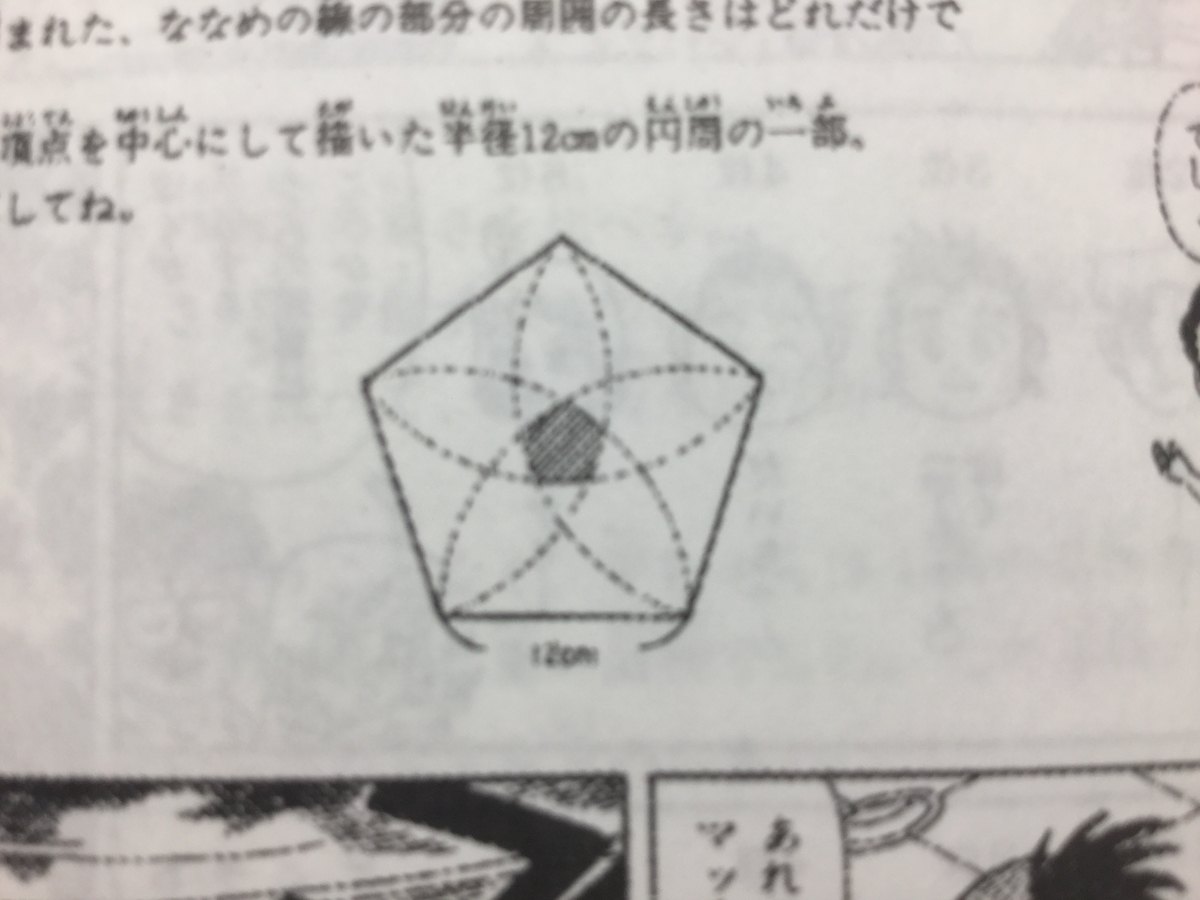
『ケーキは、ま上から見ると図のような正五角形で、点線の部分にもようが描かれている。
中央の5本の曲線に囲まれた、ななめの線の部分の周囲の長さはどれだけでしょう。
点数はすべてケーキの頂点を中心にして描いた半径12cmの円周の一部、円周率を3.14として計算してね。

』

円の問題だけど、おそらく円を作図することは無くて、その意味では最初から、円の中心から辺を追加しておいて、それぞれの辺の長さをイコールとしておくだけで良い気もする。
この問題で例えると、外側の五角形の頂点を上から反時計回りでA、B、C、D、E、また内側の五角形の頂点を同じようにF、G、H、I、Jとすると、AB == AH == AI == AEという風にするだけで良い気もする。
しかし、この問題は円の長さを答えとして求めているわけで、それでは解けない。その場合には、ちょうど問題を解ける分だけ円をデータ構造で定義する必要があるのかもしれない。
その場合は、

circle_lst := [
        [円の中心の点, [その円に属する点を適当に]],
        以下同じように続いていく
    ];

という風に定義すれば良いのではないか。弧は、例えば「⌒IAH」という風に記述する。このIAHは時計回りで、ちょうど∠IAHに対応する（なんで反時計回りで点を名付けてしまったんだろう）。

円の中心からそれぞれの点への辺は自動的にイコールで登録され、弧の具体的な長さは例えば今回だと「AI * 2 * 3.14 * ∠IAH \ 360」という風になるだろう。

今回はAIの長さは分かっているので、∠IAHの大きさが問題になる。初期条件で∠EABは、正五角形の一角、108°で登録されているので、そこから正三角形の一角の60°を2個引いて、-12°でなんとか12°だと分かるんじゃないかな、多分。

分かり次第表示するって、どう書くんだっけか？
　

96年度ファイナル問題　問題5

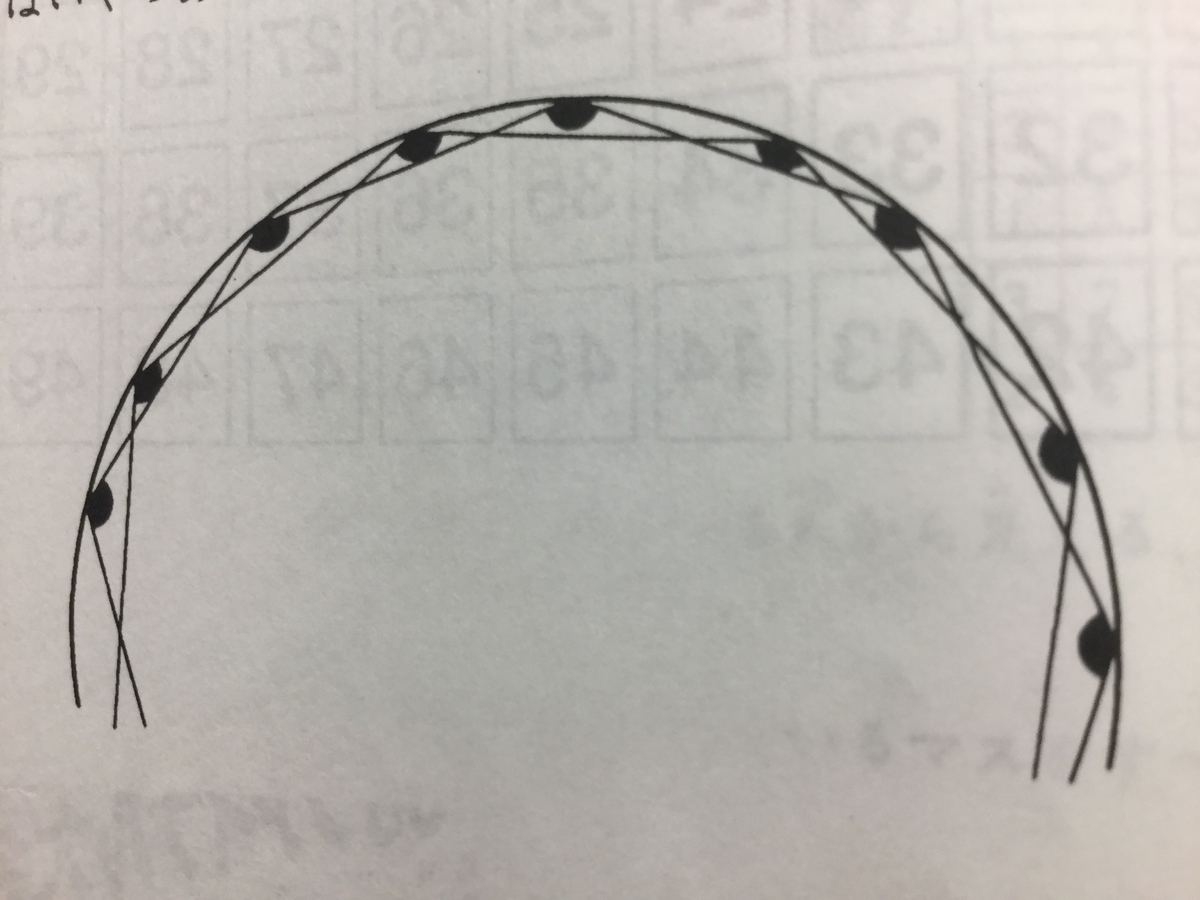
『円周上に点がいくつかならんでいます。これらの点を一つおきに直線でつないでいったところ、すべての点を通って、はじめの点にもどりました。こうしてできた図形のとがった部分の角度（図の黒い角の部分）の合計は2700度でした。
円周上に点はいくつありますか。

』

これは難しい問題で、決まった状態から別の状態というか値を弾き出すのでは無く、ルールで最初の状態を弾き出さないといけない。

答えを見ると、三角形の頂点じゃない2角は、頂点側から延長した外角と同じで、その外角がちょうど一つ飛ばした先での（への？）方向転換分の角度になっていて、それが2周分なんで720°らしい。
で頂点の合計が2700°なので、2700 + 720 == 3420°を180°で割って、19個。が答えらしい。

作図の手数の問題というより、方向転換分2周で720°、というのが分からん。分からんというのが正直な感想だ。
　

04年度ファイナル問題　問題3

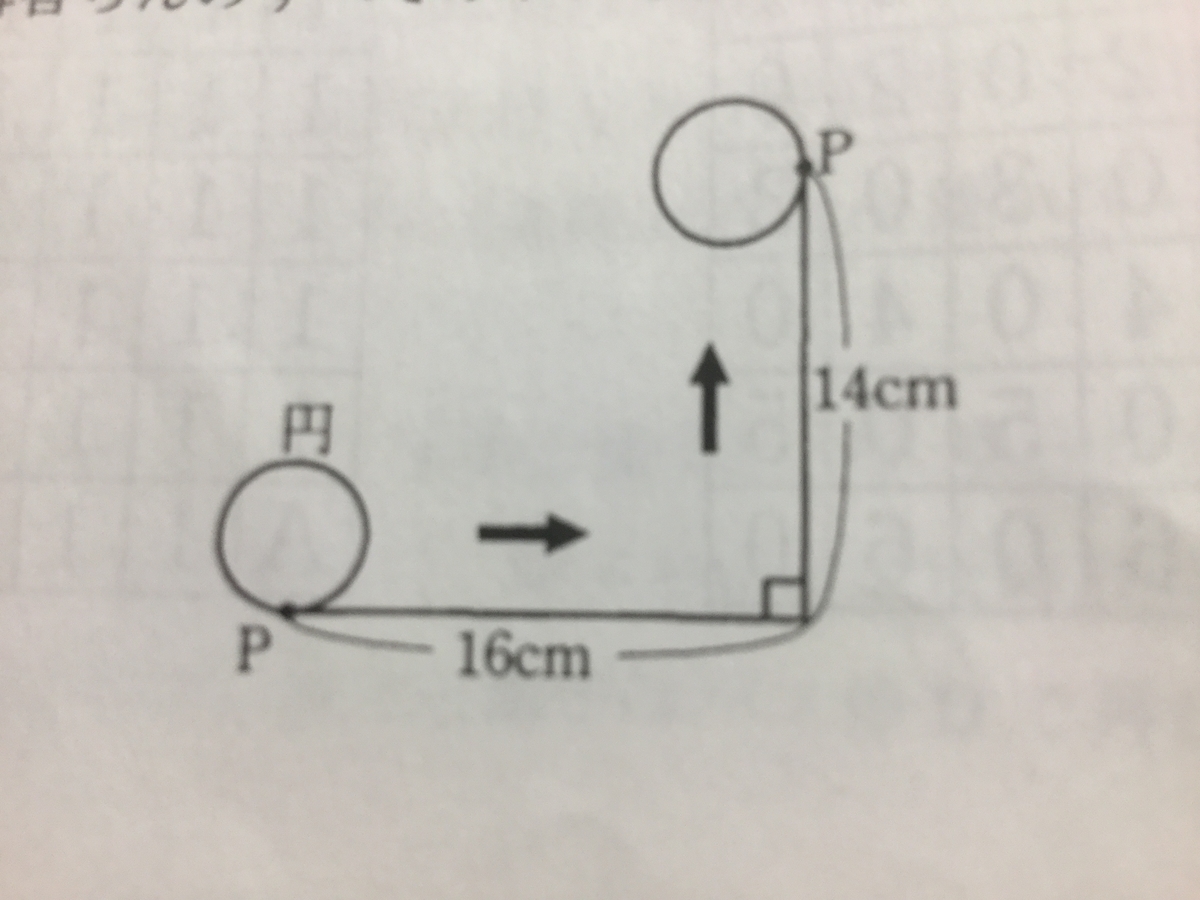
『図のように全長30cmの直角に曲がったコース上を、円がはしからはしまで離れることもすべることもなく転がりました。円周上の一点をPとし、点Pがコースのはしにふれている状態から転がり始めたところ、転がり終わったときにも、点Pがコースのはしにふれていました。また、転がり始めと転がり終わり以外で、点Pがコースにふれたことはありませんでした。
このとき、円の半径は何cmでしょうか。円周率は3.14として、答えが割り切れない場合は、小数第三位を四捨五入しなさい。また、もし答えが複数ある場合は、それらをすべて書きなさい。
ただし、解答らんのすべてのワクを使うとは限りません。

』

これは転がるという動きがあるので、どちらかというと昔やった連続的な問題という奴なのかと思う。いやある一定のスピードで加算されていくというわけじゃないから、そうでは無いのか。答えを見た。

完全に右の壁に接触するまでは、下の床？ - 半径だけ転がる。右の壁を転がる時には、右の壁 - 半径だけ転がる。

もし右の壁に接触した時に、隅っこの「円周/4」の所に点が無いなら、「円周 * 3 / 4 == 下の床の長さ - 半径 + 右の壁の長さ - 半径」。

もし隅っこに点があったなら、「円周 * 7 / 4 == 下の床の長さ - 半径 + 右の壁の長さ - 半径」だろう。

こういうただ式を立てる問題は、ジャンル分けするなら代数学なのかなと思う。
　

05年度ファイナル問題　問題1

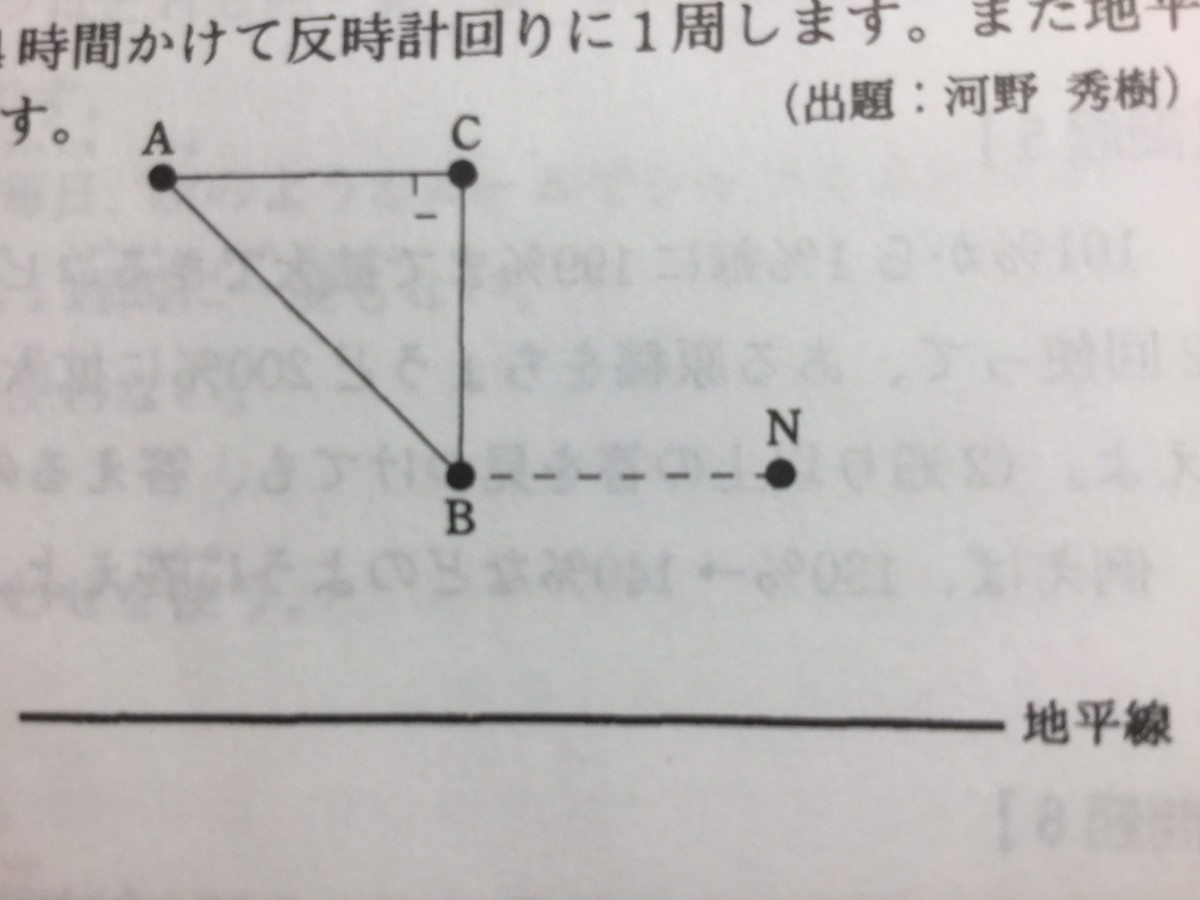
『午後6時30分北の空に北極星Nと直角二等辺三角形の形になる星A、B、Cが図のように見えました（Nの左にB、Bの上にC、Cの左にAで、NB=BC=CA）。
何時間か後に星Aと星Bが同時に地平線に沈みました。そのあと星Cが沈みました。星Cが沈んだ時刻を求めなさい。ただし、星A、B、Cは北極星の周りを24時間かけて反時計回りに1周します。また地平線は水平な直線とします。

』

答えを見た。この問題は難しいな。

解答のプロセスは2段階に分かれていて、まず、ACNBをクラスタと見なして、Nを共有して、また新しい方のAとBが地平線の上にあるようなのを作図する。そうすると、新しい方の角BNCが45°だと分かる。（新しいCNと地平線が平行だとも分かるらしい。）
星は北極星を中心に一時間に15°回転すると書いてあるので、3時間分だと分かる。

新しいCNから、更に新しいCNを平行線上に更に新しいCが来るように作図する。
2番目のCから垂線を下ろすと、（答えの図を見ながら書いているが）二等辺三角形が発生して、2番目のCNの半分の長さだと分かる。
2番目のCN == 更に新しいCN、かつ、2番目のCからの垂線 == Nからの垂線。これで更に新しいCNと、その垂線の比率が明らかになって、なんか直角だと（厳密にはピタゴラスの定理）で比率というか三角形の種類で角度が分かって、頂点側が60°だと分かる。
で、地平線だとかそういうので、2番目のCNと最後のCNの角度は30°だと分かって、2時間進んだと分かる、らしい。

それで答えは5時間。

時間の進みがあって、しかも2段階に分けて答えなきゃいけないのが嫌だったな。2つのACNBを設定して、地平線上にCがある更に新しいCNを設定すれば、色々なCNの角の足し算を答えになるように設定しておけば自動で出たりしたのかな。

分からないな。まあ参考にする感じで見返しにこれば良いと思うけど。