00年度ファイナル問題 問題4
『一辺の長さが15の正六角形の板が1枚と半径1の円板がたくさんあります。いま、正六角形の板を机の上に置きそのまわりに半径1の円板を次の条件をみたすように置いていきます。
(ア)板は、重ねて置いてはいけない。
(イ)すべての円板は、正六角形板と1点で接する。(角で接していても良い)
(ウ)隣りあう円板どうしは、接していても接していなくてもよい。
このとき、円板は最大で何枚並べることができますか。
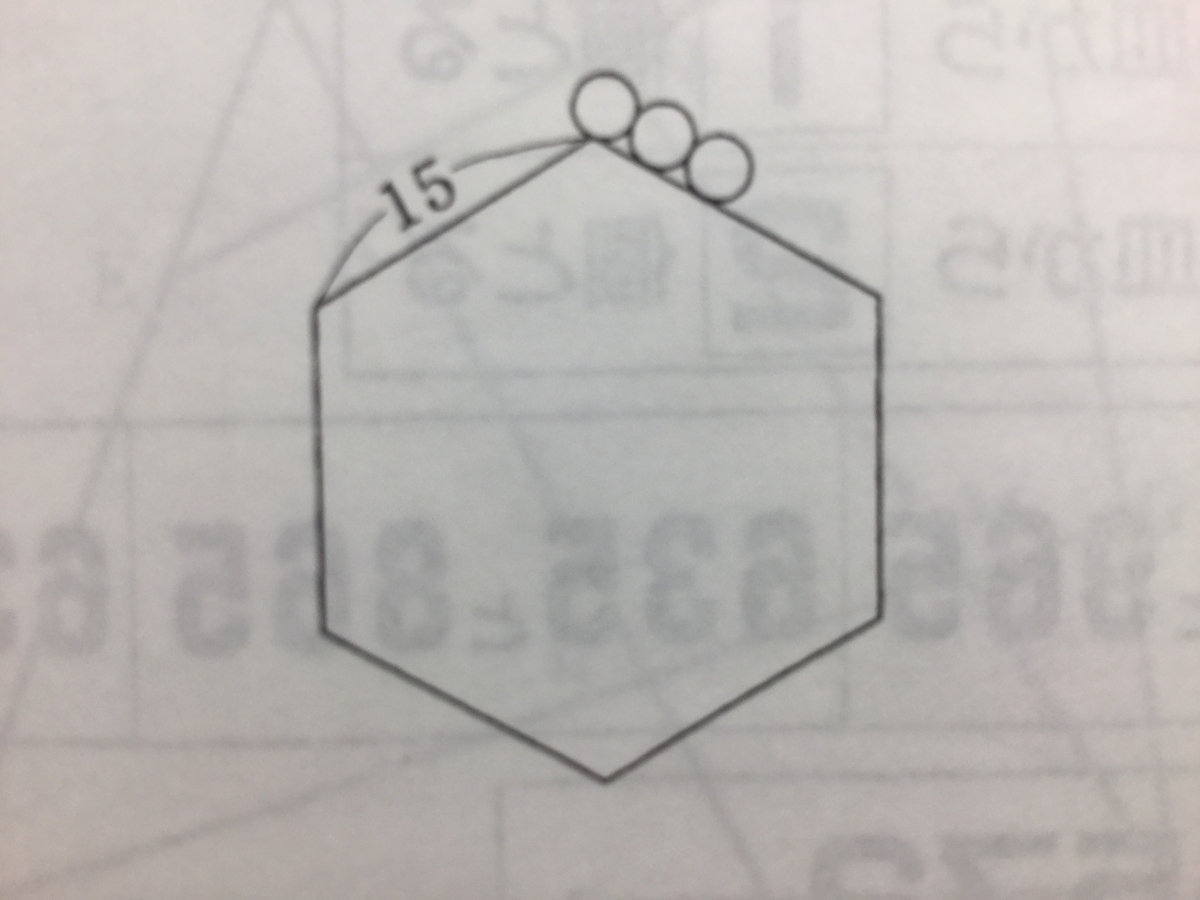 』
』
最後に記述できなかった問題を書き残しておく。
『一辺の長さが15の正六角形の板が1枚と半径1の円板がたくさんあります。いま、正六角形の板を机の上に置きそのまわりに半径1の円板を次の条件をみたすように置いていきます。
(ア)板は、重ねて置いてはいけない。
(イ)すべての円板は、正六角形板と1点で接する。(角で接していても良い)
(ウ)隣りあう円板どうしは、接していても接していなくてもよい。
このとき、円板は最大で何枚並べることができますか。
 』
』
『半径2の円板O’上に、中心からの距離が1の定点Pがあります。円板O’を半径4の円Oに内接させながら転がすとき、点Pが動く図形によって囲まれる部分の面積を求めなさい。
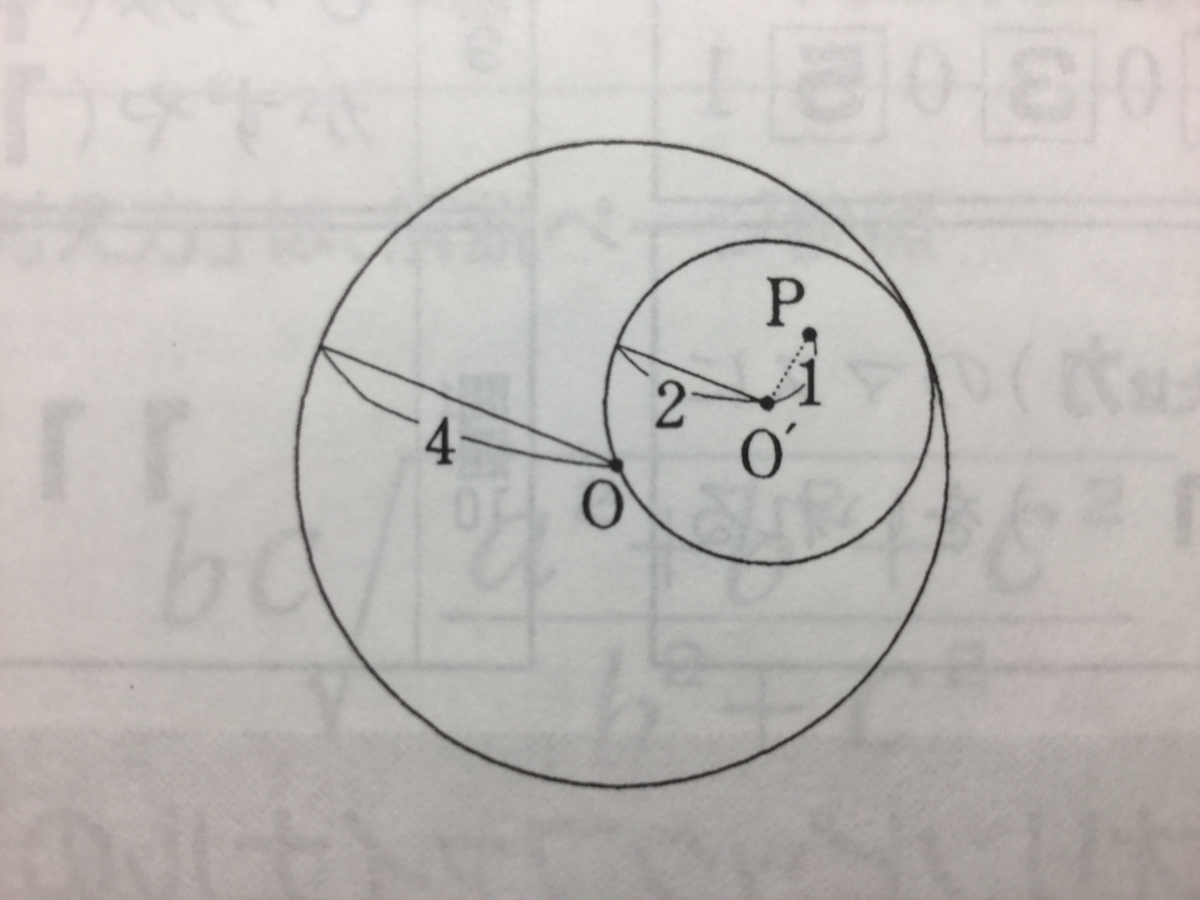 』
』
『たとえば、1辺の長さが1の正6角形の各辺の外側に、1辺の長さが1の正6角形を1つずつくっつけると、くっつけた正6角形のとなりあう2つは1辺を共有する。
1辺の長さが1の正m角形の各辺の外側に1辺の長さが1の正n角形を1つずつくっつけたとき、くっつけた正n角形のとなりあう2つが1辺を共有するようなm、nの組として考えられるものをすべて求めなさい。(m,n)=(6,6)のように答えよ。(解答例以外の組を答えなさい。)
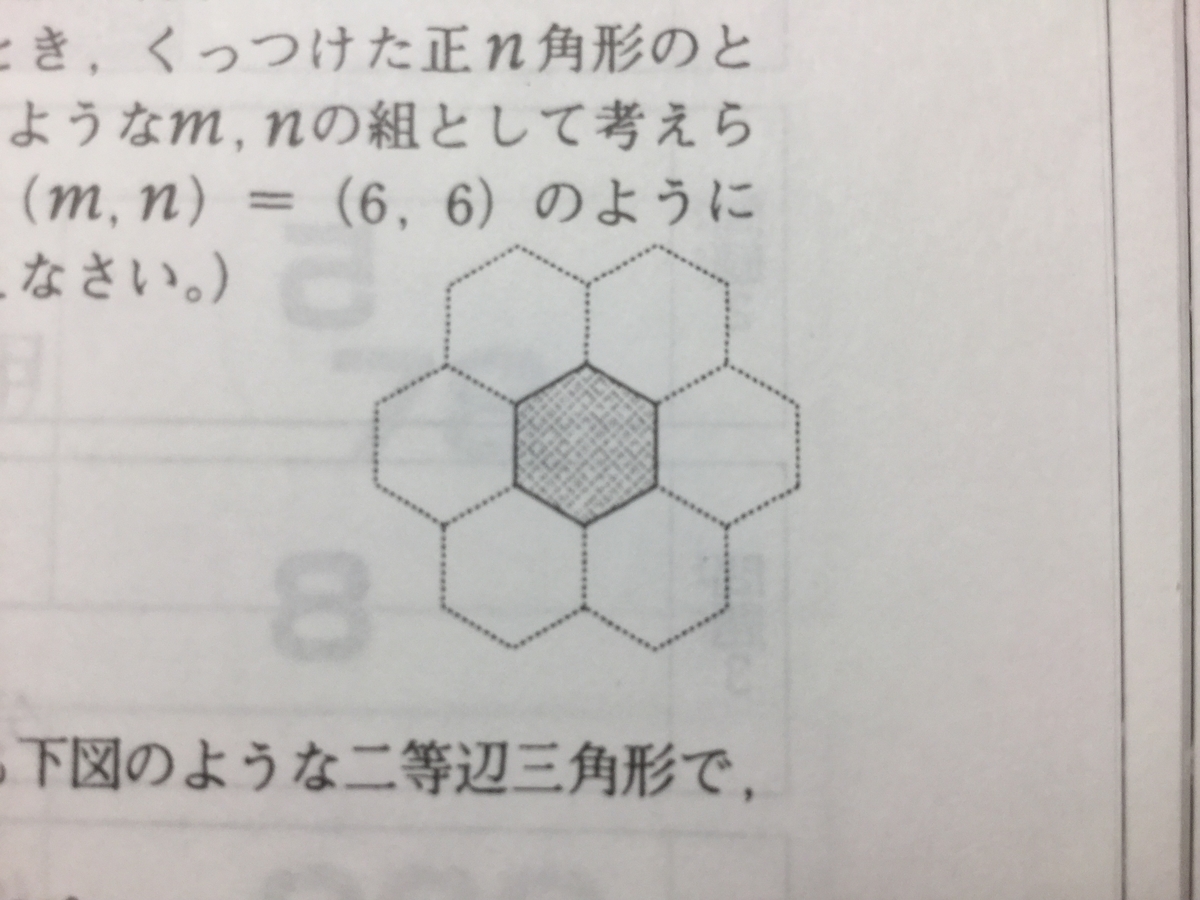 』
』
『半径1、高さ1の円柱がある。上面の円周の4等分点をA、B、C、D、中心をOとし、ACを含む底面と45°の角をなす平面、およびBDを含む底面と45°の角をなす平面による円柱の側面の切り口を図のようにC1、C2とする。
C1、C2の交点をPとするとき、線分OPの長さを求めよ。
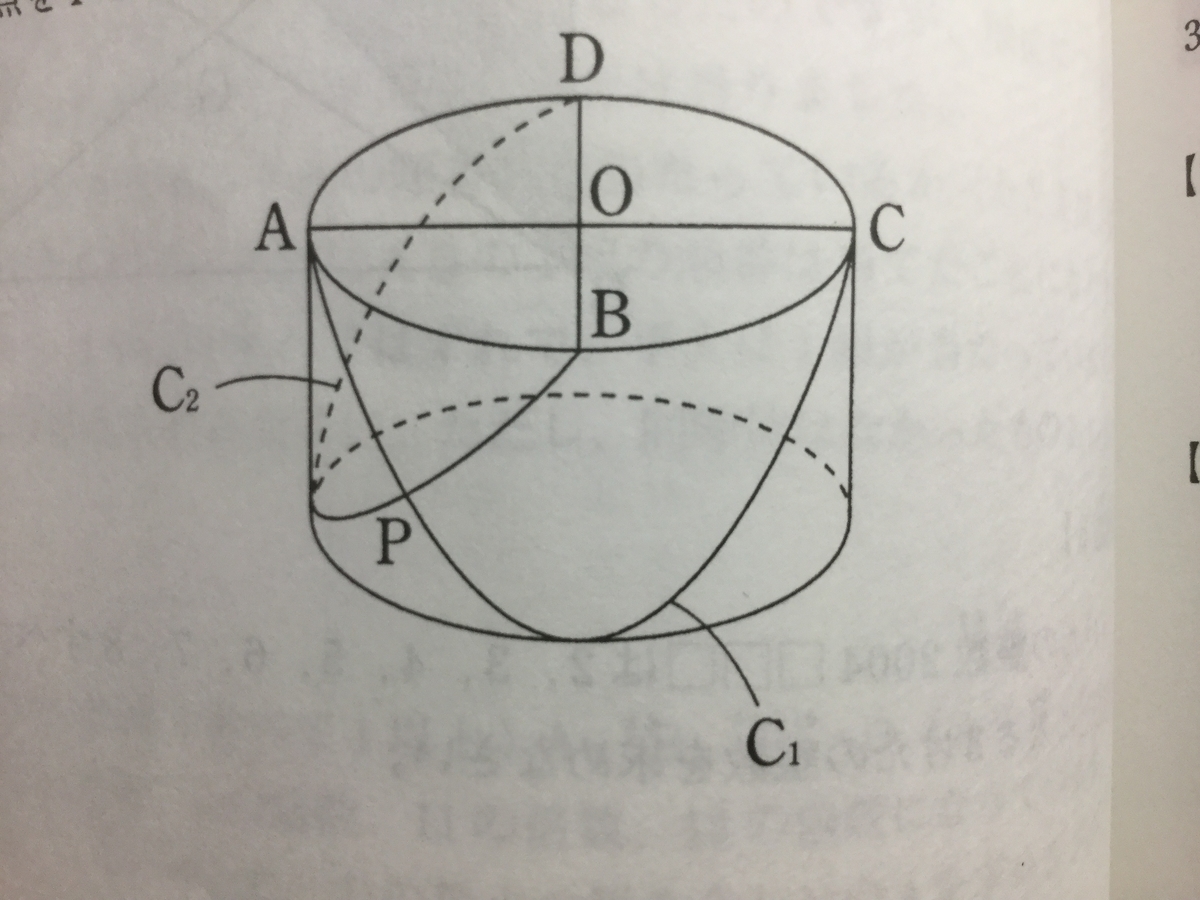 』
』
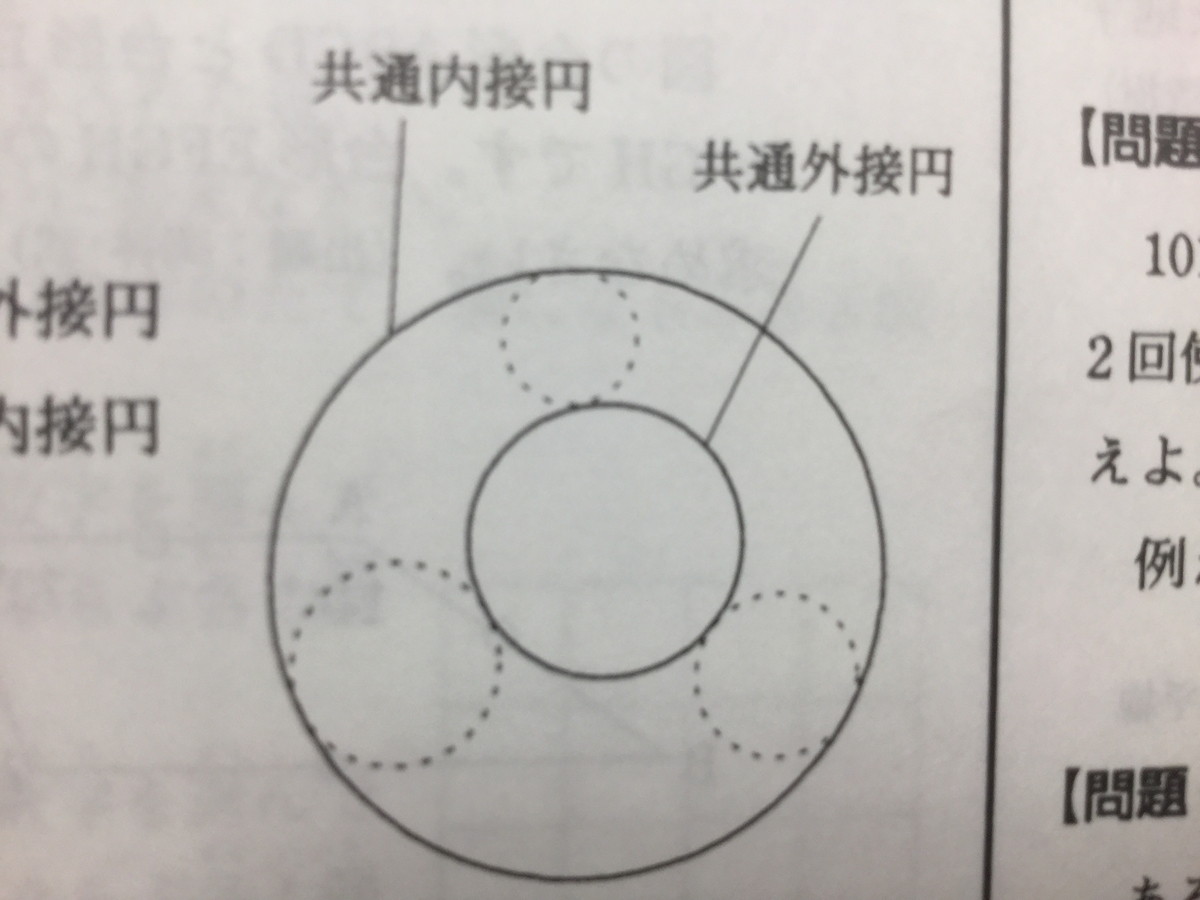
『互いに交わらない3つの円があるとき、
その3円全てと外接する円を、3円の共通外接円
その3円全てと内接する円を、3円の共通内接円
と呼ぶことにする。(右図参照)
(1)3つの円があり、
・各々の円の半径は1
・3円の中心をA、B、Cとしたとき、AB=3、BC=4、CA=5
であるとする。この3円の共通外接円の半径を求めよ。(答のみで良い)
(2)一辺の長さが8の正三角形XYZがある。
Xを中心とする半径2の円をC1
Yを中心とする半径3の円をC2
Zを中心とする半径4の円をC3
とするとき、C1、C2、C3の共通内接円の半径Rと共通外接円の半径rの差R−rを求めよ。
ただし、C1、C2、C3に、共通内接円、共通外接円がそれぞれただ一つ存在することは、証明無しに用いて良い。
(考え方の欄に途中の考え方を、答の欄に答を記しなさい。途中の考え方も採点対象になります。)』
『一辺の長さが4で、内角の一つが30°であるひし形がある。このひし形を、ある一辺の周りに1回転させることによってできる立体の体積を求めよ。』