04年度ファイナル問題 問題1
『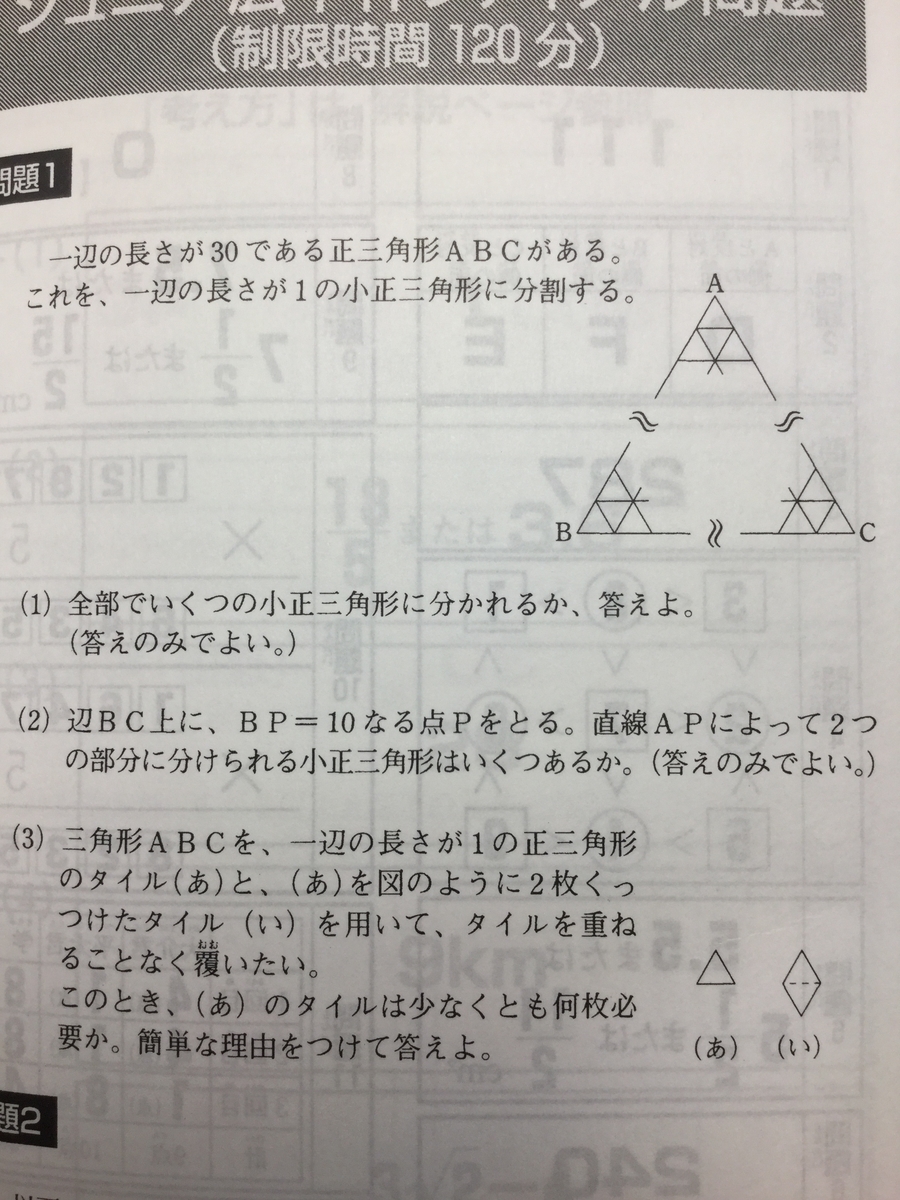 』
』
最後に記述できなかった問題を書き残しておく。
『 』
』
『図のように、半径の異なる2つの円C、Dが直線lに接している。C、D、lの全てに接する円はいくつあるか?
ただし、C、Dは共有点を持たず、またC、Dの中心はlに関して同じ側にあるものとする。
(注)2つの円が接するとは、2円が共有点をただ一つ持つことを、円と直線が接するとは、円と直線が共有点をただ一つ持つことをそれぞれ表している。
 』
』
『図1の様に、7×7の正方形のマスと、「マスS」、「マスG」がくっついたものがある。マスは、全て1辺の長さが1の正方形である。
Sの中心からGの中心まで、点Pが全てのマスをちょうど1回ずつ通って移動する。
ただし、Pは水平方向か上下方向にしか移動せず、距離1だけ進むごとにのみ方向を変えることができるものとする。
このときの点Pの軌跡をマスに書き込んだ結果、「まっすぐな線」のみが残っている(マスS、G以外の)マスの個数をXとする。
例えば、図2の様に移動した場合、X=21となる。
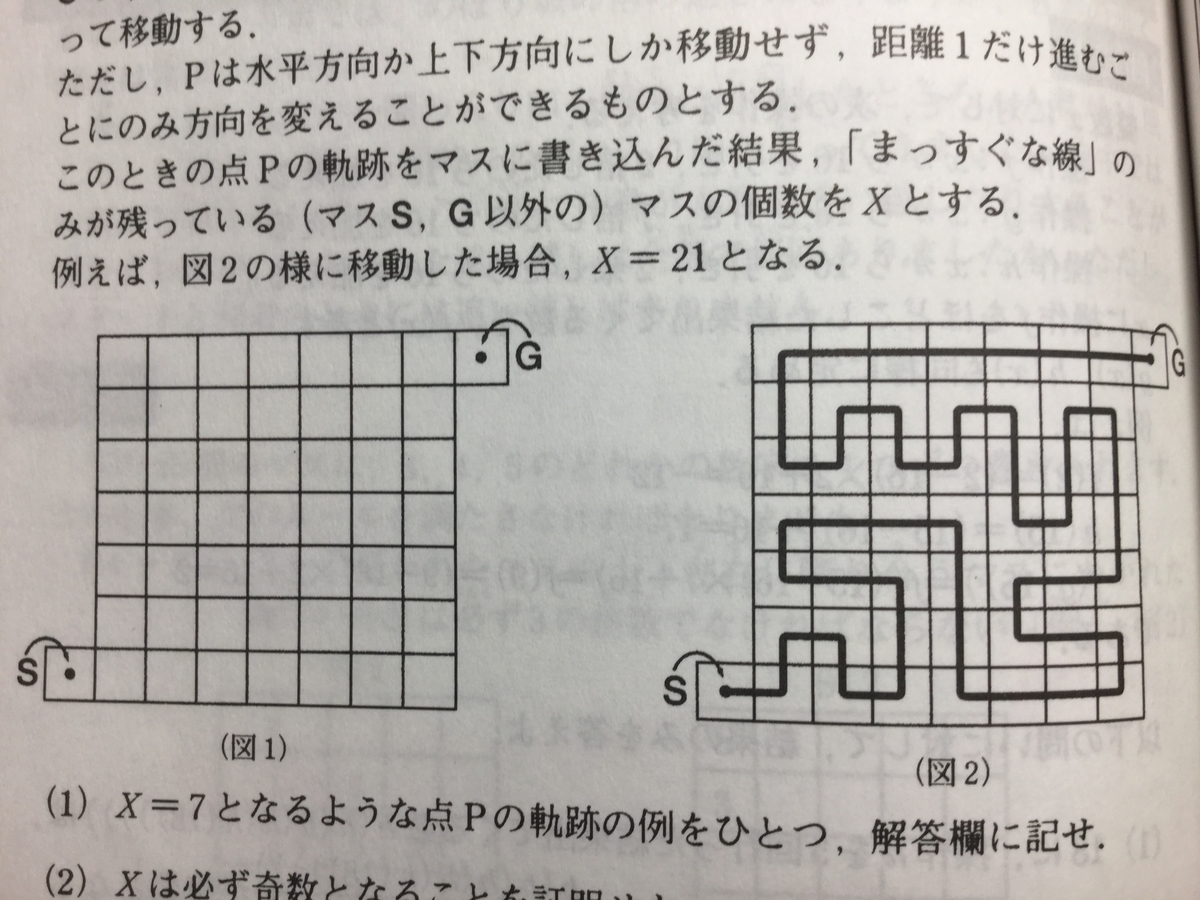
(1)X=7となるような点Pの軌跡の例をひとつ、解答欄に記せ。
(2)Xは必ず奇数となることを証明せよ。
(3)Xは5以下となることはない。そのことを証明せよ。』
答えに必要な理由が多分抽象的な問題。
『平面上に、異なる8個の点を次の性質を持つように配置できるだろうか?できるならそのような一例を挙げ、説明せよ。できないならその理由を説明せよ。
(性質)8個の点のどの2点を結んでも、その線分の垂直二等分線上に、8個の点のうちの少なくとも2点が存在する。』
この問題もそうなのかな?よく分からないけど。