このページの問題を、基本的には上から解いていこうかと思っている。
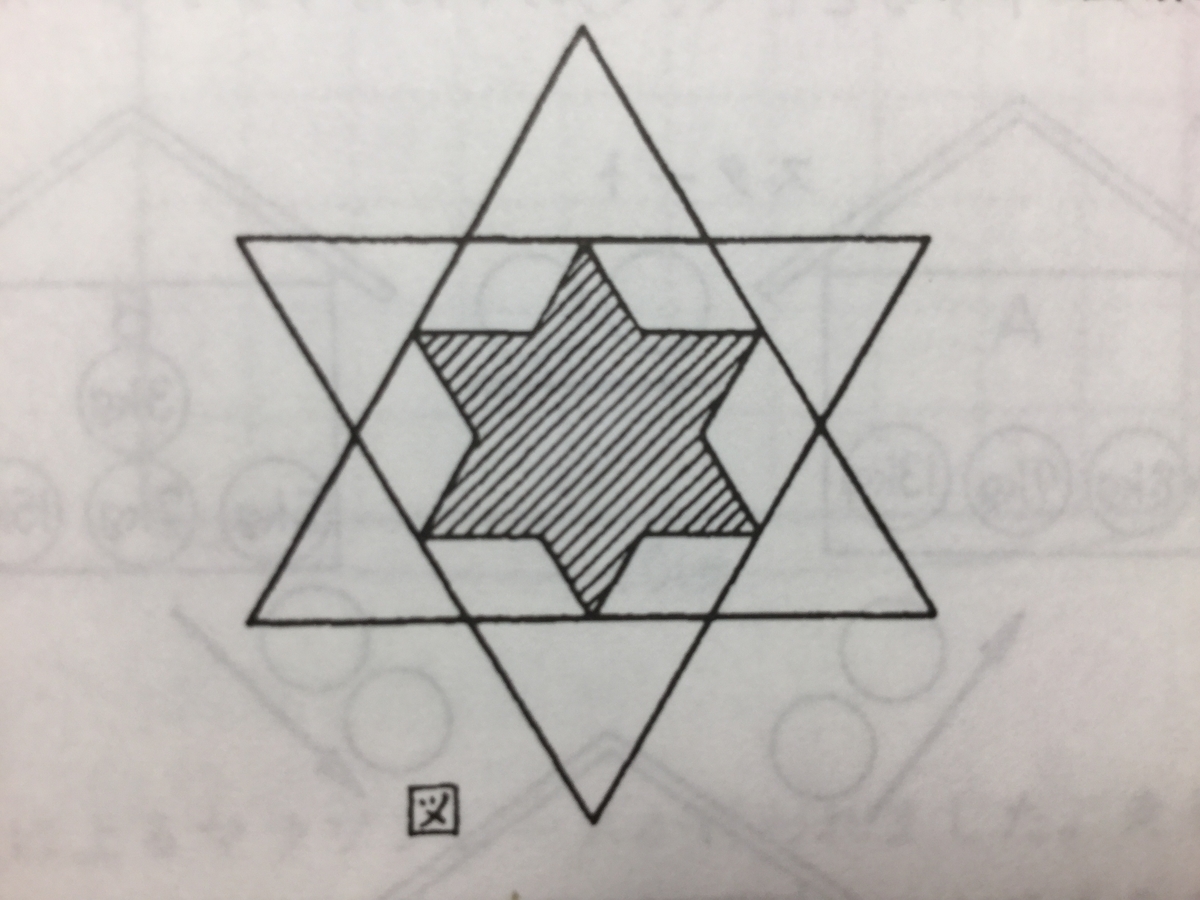
『大きな正三角形を2つ重ねて星型の12角形を作り、その中に同じように小さな星型の12角形（図の斜めの線の部分）を作りました。大きな星型の12角形の面積が72cm^2のとき、小さな星型の12角形の面積は何cm^2ですか。
』
解答を見ると、外側の三角6つと中の六角形は同じで、六角形の中も空白部分のピースで敷き詰める形で12角形を再現して、大きな星型72cm^2 \ 2 \ 2 == 18cm^2、という風に解答している。
ただ、俺が思うに一つだけ条件の指定が弱くて、正三角形同士の重なり方を変えれば、中の12角形は潰れていって面積も少なくなっていく。
その、例えば12角形の全ての辺がイコールで、中の12角形も同じで、という風に初期条件を登録できれば、解けると思う。
一つ一つの三角形は二等辺三角形でつまり正三角形で、中の正六角形も分割すると合同で、中の12角形も正三角形を重ねた形なので、という感じ。
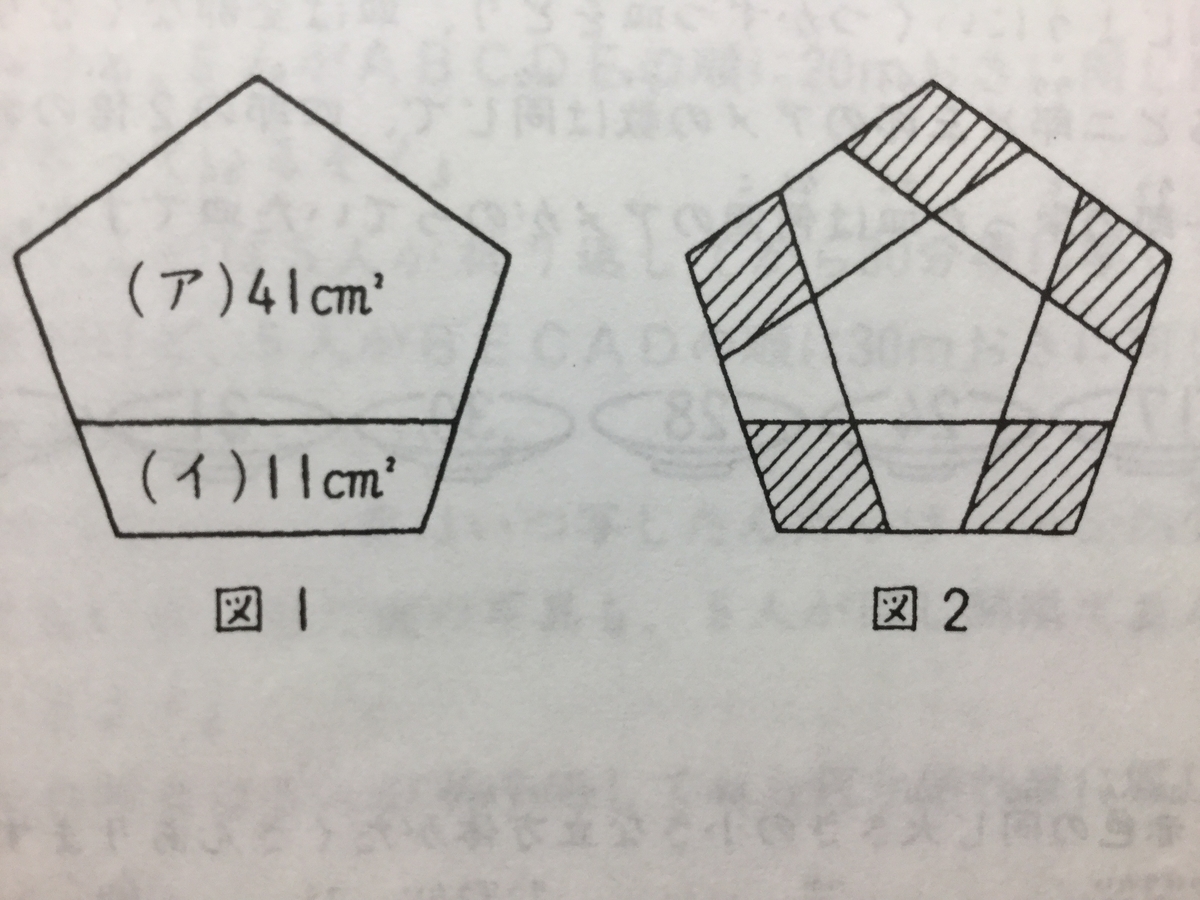
『図1は正五角形を（ア）と（イ）の2つの部分に分けたもので、（ア）の面積は41cm^2、（イ）は11cm^2です。（イ）は台形です。
図2は図1の（イ）の部分と同じものを5枚つくり、図1の上に重ねたものです。図2の斜めの線の部分の面積の和は、まん中にできた小さな正五角形の面積より、何cm^2大きいですか。
』
まず、「[[頂点, 辺, 頂点, 辺, 頂点, 辺, 頂点, 辺, 頂点, 辺], 真ん中]」、という風な循環リストを考える。それぞれの頂点だとか辺だとか真ん中だとかは変数だ。
そして、どこかの「頂点, 辺, 頂点」にそれぞれ1足すか引くか、どこかの「辺, 頂点, 辺, 頂点, 辺, 頂点, 辺」と「真ん中」にそれぞれ1足すか引くかして、前者であれば「答え」という変数に11足すか引くかして、後者であれば41足すか引くかする。そういう風にステップを定義する。
で、もちろん答えを見たのだけど、全ての変数の初期値を0にして、状態が「[[1, 0, 1, 0, 1, 0, 1, 0, 1, 0], -1]」の時に「答え」がどうなるかを問うている、と考えれば良いみたいだ。
問題を説明するための図2が同時にヒントにもなっていて、図2の状態から全体を引けば、そのまま答えになるらしい。