記述できなかった問題 その1 ジュニア算数オリンピック 三次元ユークリッド幾何
最後に記述できなかった問題を書き残しておく。
面と面でどこに交点というか交線ができるかが課題だろうが、ホッチキスの針みたいに辺の集まりのように考えれば良いんじゃないか。クラスタの出っ張っている部分は、そこまでは辺は無いものと考える。
おそらく完全に平行な場合と三角錘の場合の2通りがあり得るだろう。三角錘の場合は、どこか1点でも交点が分かれば、そこから頂点側の端点まで線を引いて、それから(1対1にならない気がしているけど)お互いの比率でお互いがその線に達していたら、そこには接点ができて、集まれば接線ができる。と考えることができるんじゃないか。
面と辺の交点は、分からない。
97年度トライアル問題 問題5
『立方体の各辺の半分の長さの点を結んで、各頂点から三角すいを切り落とすと、見取り図のような正三角形と正方形で囲まれた美しい立体図形、(アルキメデスの準正多面体)が出来上がります。
この図形の展開図は、図①、図②のようになります。

(問い1)図①の展開図を組みたてたとき(A)の面と平行なのは、(B)の面です。では、(ア)の面と平行なのは、(イ)(ウ)(エ)(オ)(カ)(キ)(ク)のどの面ですか。
(問い2)図②の展開図を組みたてたとき、辺アイと平行な辺に線を引きなさい。(1つの辺が、2つに離れている場合は、両方に引きなさい。)』
97年度ファイナル問題 問題5
『たて、横、高さが、それぞれ1cmの小さい立方体27個使って、右の図のような大きい立方体を作りました。
この大きい立方体をA、B、Cの3つの点を通るような平面で切断したとき、次の問いに答えなさい。
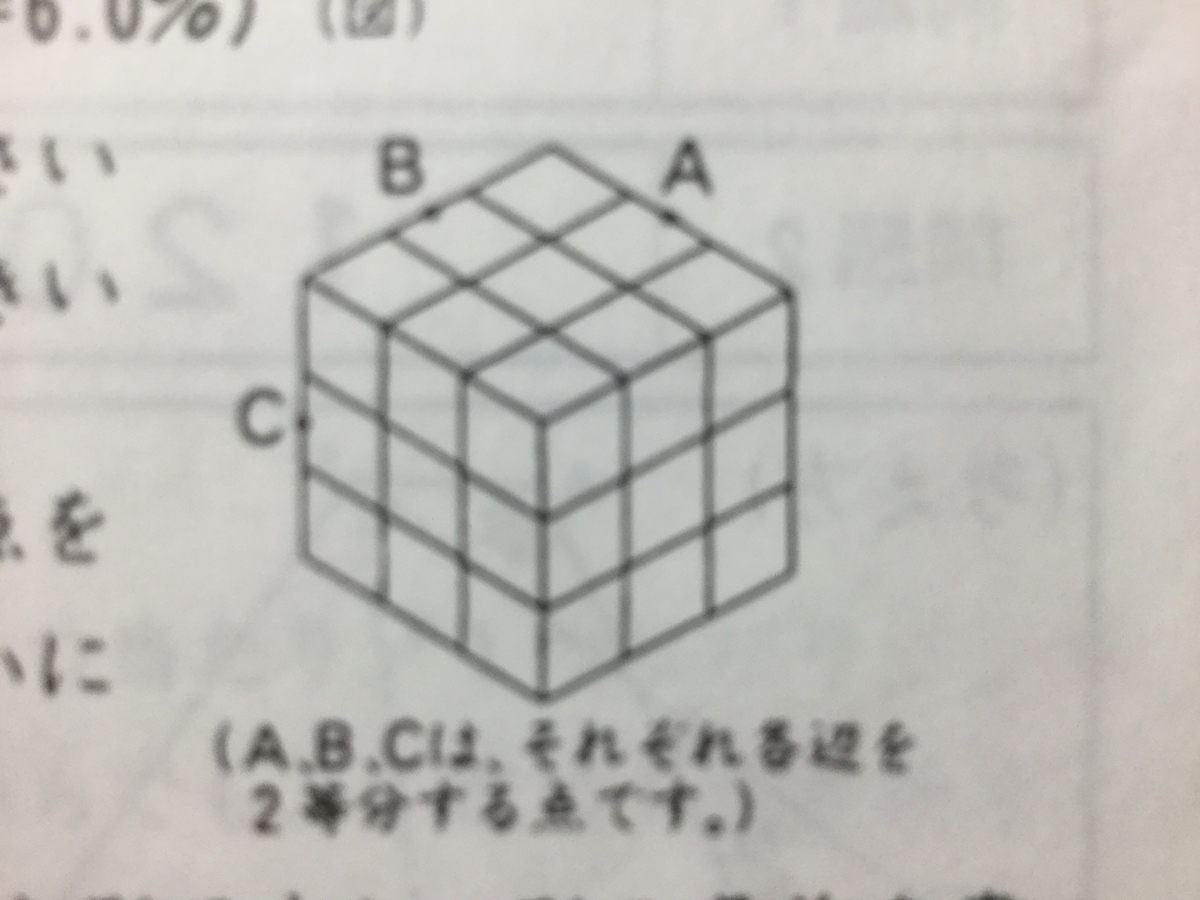
(問い1)大きい立方体の切断面はどんな形ですか。形の名前を書きなさい。
(問い2)この平面によって、小さい立方体は全部で何個切断されているでしょうか。
ただし下の図のように小さい立方体の頂点、辺、面が切断面とふれているだけのものは、切断されていないものとして考えなさい。
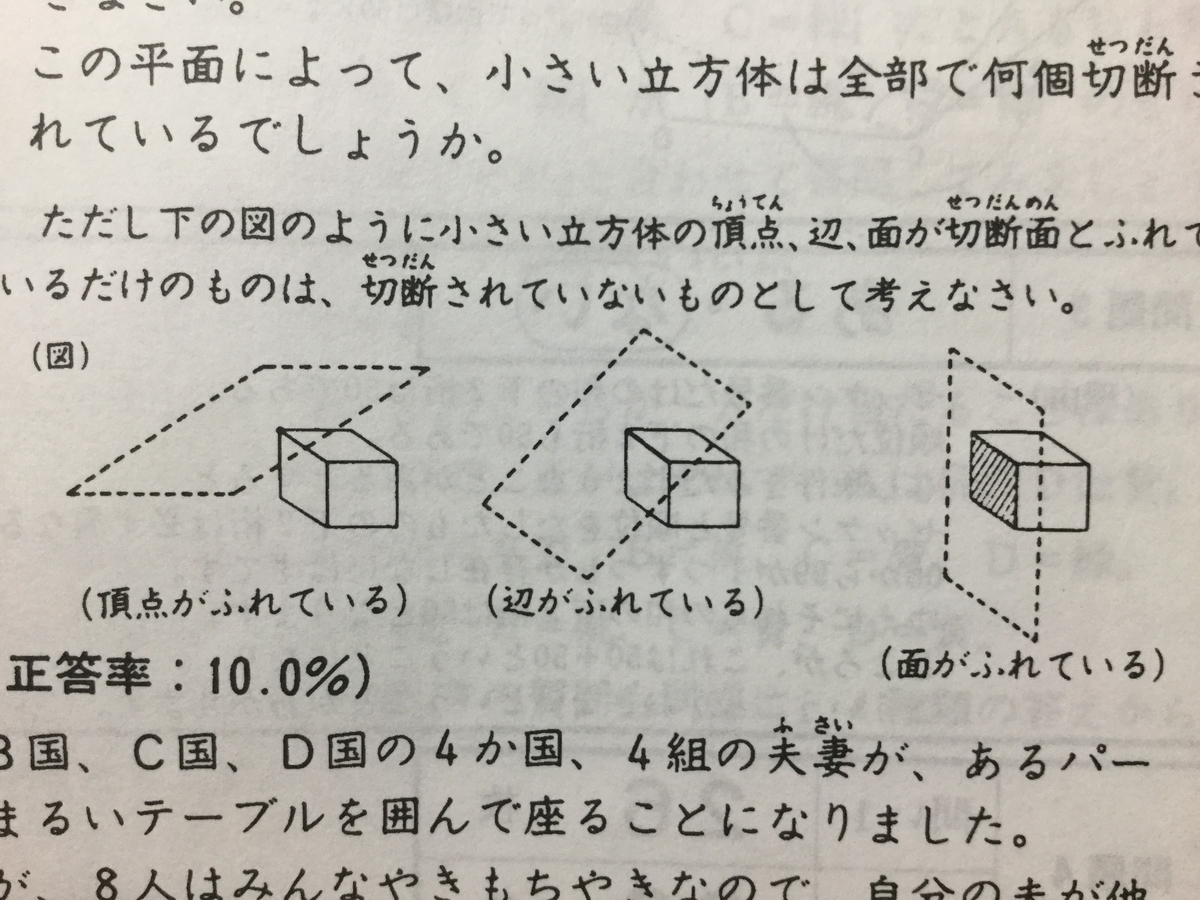 』
』
03年度ファイナル問題 問題7
『右の図の立体ABCD-EFGHは直方体の箱で、たてが1m、横が1m、高さが2mです。この箱にまっすぐな棒を、一方の端が頂点Gに来るように置いたところ、もう一方の端は辺AEのちょうど真ん中の位置Iに来ました。
棒の太さは考えないものとして、次の問いに答えなさい。
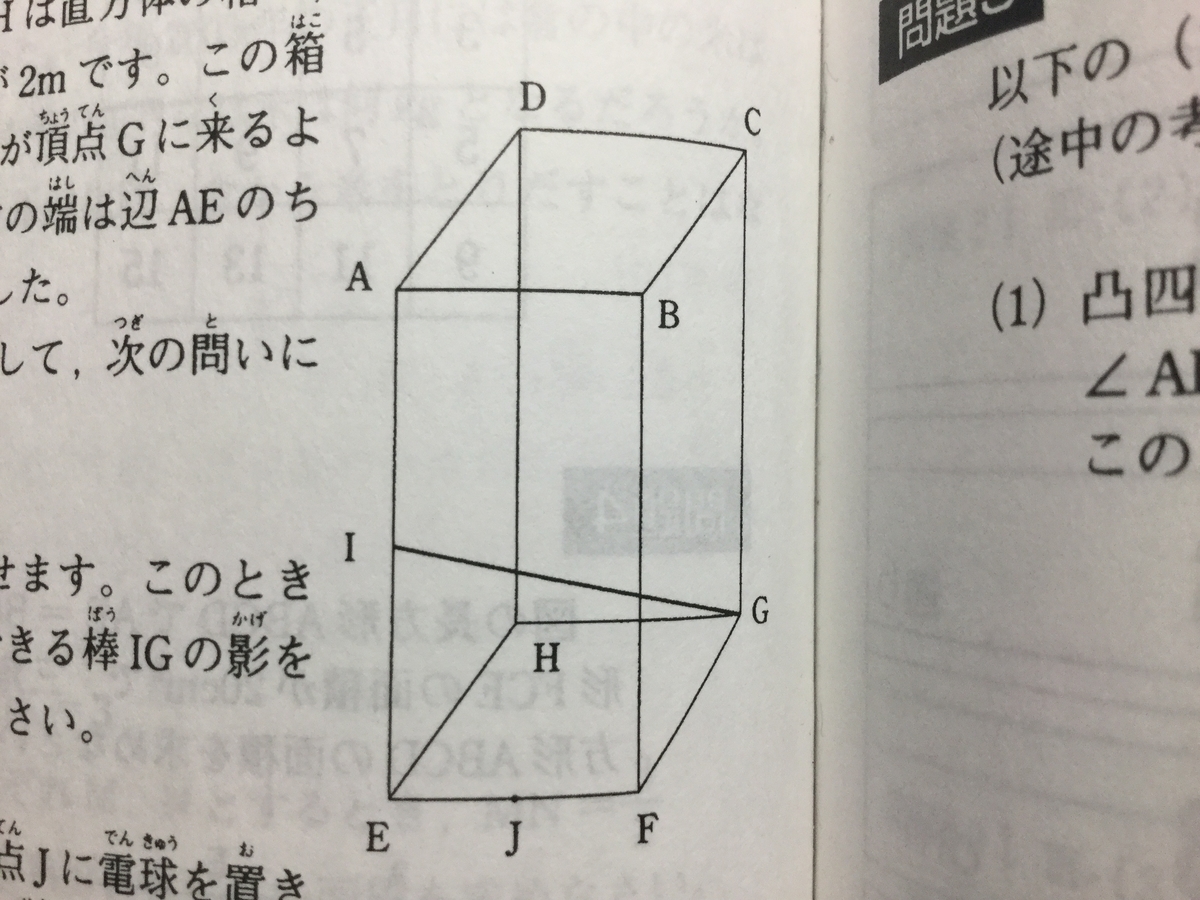
(問い1)
点Fに電球を置き点灯させます。このとき面AEHDと面DHGCにできる棒IGの影を解答用紙の図にかき入れなさい。
(問い2)
辺EFのちょうど真ん中の点Jに電球を置き点灯させます。このとき面AEHDと面DHGCにできる棒IGの影を解答用紙の図にかき入れなさい。』
09年度トライアル問題 問題11
『同じ大きさの小さな立方体27個で図1のような大きな立方体を作りました。
いま、細く長いまっすぐな針金を何本か使って、すべての小さな立方体をさします。
最低何本の針金が必要でしょうか。ただし、針金の太さは考えないものとします。
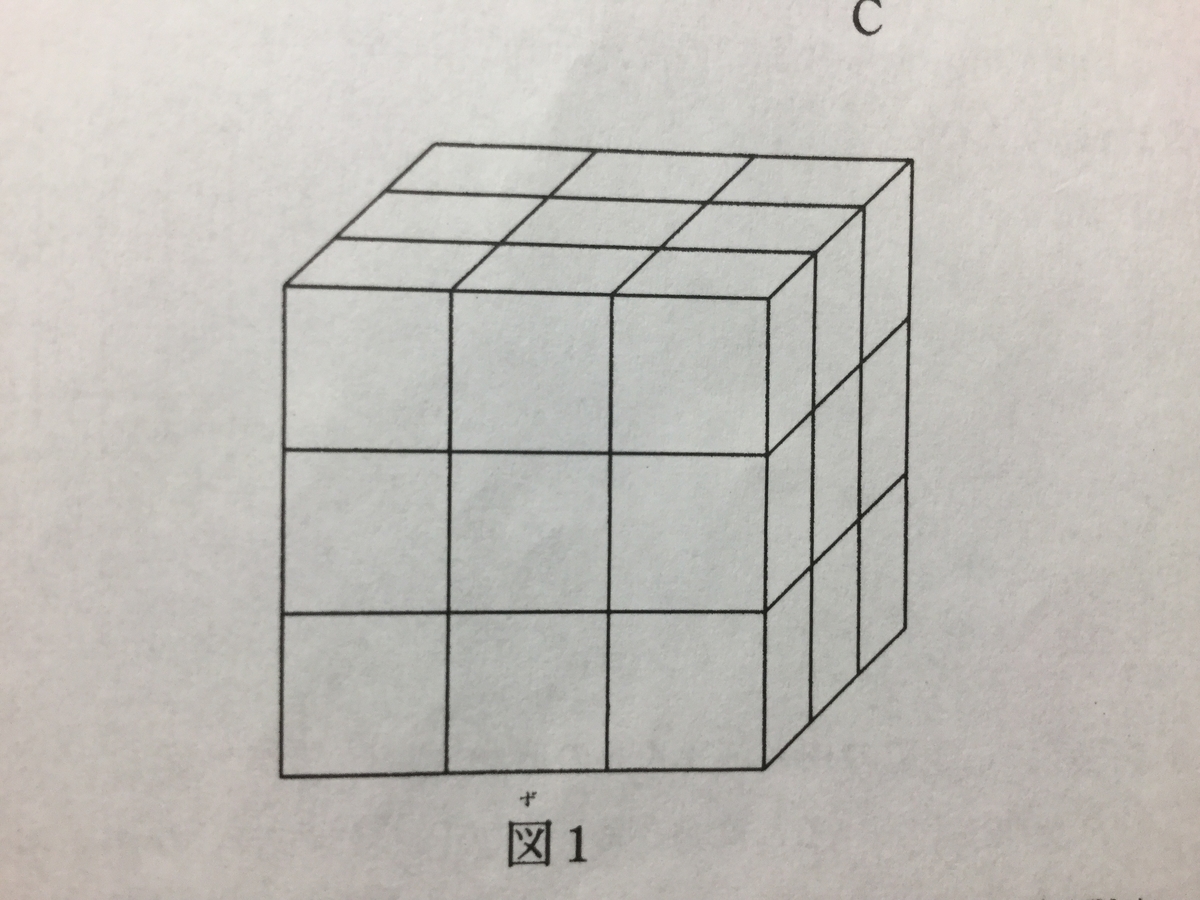 』
』
12年度ファイナル問題 問題4
『4つの面に囲まれた立体のことを四面体といい、四面体のすべての辺が等しい立体のことを正四面体とよびます。正四面体ABCDの各頂点から対面に下ろした垂線4本は1点で交わることがわかっています。この点をHとし、Aから対面に下ろした垂線の足をEとすると、AH=EH×3となりました。
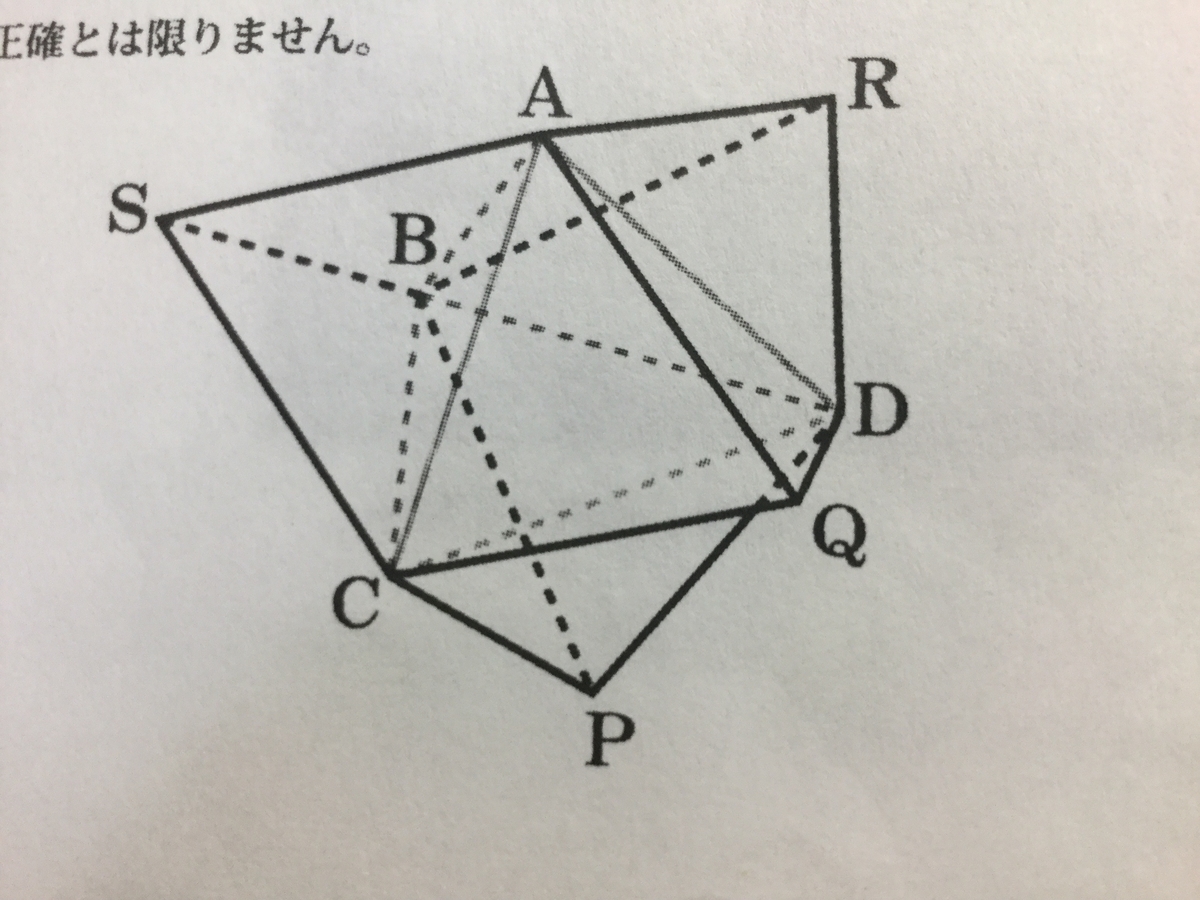
いま、一辺が1cmの正四面体ABCDの外側に1辺が1cmの4つの正四面体PBCD、QACD、RABC、SABCを配置するとき、4点P、Q、R、Sを結んでできる立体PQRSもまた正四面体となります。
正四面体PQRSの一辺の長さを求めなさい。
※ただし、図は正確とは限りません。
 』
』


 』
』
 』
』 』
』